Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
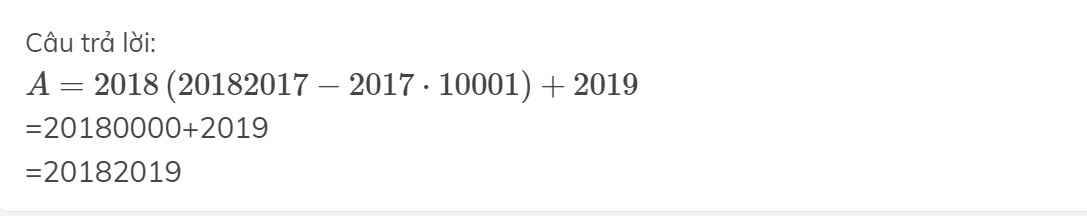
\(A=2018\left(20182017-2017\cdot10001\right)+2019\)
=20180000+2019
=20182019
A = 2018 . 20182017 - 2017 . 20182018 + 2019
= 2018 . 20182017 - 2017 . 10001 . 2018 + 2019
= 2018 . (20182017 - 20172017) + 2019
= 2018 . 10000 + 2019
= 20182019
Không bt có đúng ko nx 
A \(=\dfrac{2017.20182018}{2018.20172017}\)
ta có : 2017.20182018 = 2017. (2018. 10000 + 2018)
= 2017 . 2018.10000 + 2017 . 2018
2018.20172017 = 2018. (2017. 10000 + 2017)
= 2018 . 2017.10000 + 2018 . 2017
Vậy A \(=\dfrac{2017.20182018}{2018.20172017}\)\(=\dfrac{\text{2017 . 2018.10000 + 2017 . 2018}}{\text{2018 . 2017.10000 + 2018 . 2017}}\)\(=1\)
Cho a,b,c dương thỏa mãn : a+b+c=2019
Tính A = \(\frac{a}{2019-c}+\frac{b}{2019-a}+\frac{c}{2019-b}\)
Thiếu dữ kiện, nếu chỉ cho vậy thì không tính đc gt cụ thể của A
+ Làm theo đề là tìm Min của A nhé!
\(A=\frac{a}{2019-c}+\frac{b}{2019-a}+\frac{c}{2019-b}=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}.\)
\(A+3=\frac{a+b+c}{a+b}+\frac{a+b+c}{b+c}+\frac{a+b+c}{c+a}=\left(a+b+c\right)\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\)\(\ge\left(a+b+c\right)\frac{9}{2\left(a+b+c\right)}=\frac{9}{2}\)(BĐT Bunhia)
Dấu "=" xra khi a=b=c=2019/3
\(\frac{2019}{1\times2}+\frac{2019}{2\times3}+\frac{2019}{3\times4}+...+\frac{2019}{2018\times2019}\)
\(=2019\left(\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{2018\times2019}\right)\)
\(=2019\left(\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2018}-\frac{1}{2019}\right)\)
\(=2019\left(1-\frac{1}{2019}\right)\)
\(=2019\left(\frac{2019}{2019}-\frac{1}{2019}\right)\)
\(=2019\times\frac{2018}{2019}\)\(=\frac{2019\times2018}{2019}=2018\)
