Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

#include <bits/stdc++.h>
using namespace std;
int B[100],n,t;
{
cin>>n;
for (int i=1; i<=n; i++) cin>>B[i];
t=0;
for (int i=1; i<=n; i++)
if (B[i]%10==0) t+=B[i];
cout<<t<<endl;
int dem=0;
for (int i=1; i<=n; i++)
if ((i%2==0) && (A[i]%2!=0)) dem++;
cout<<dem<<endl;
for (int i=1; i<=n; i++)
if ((A[i]%2!=0) && (A[i]%3==0)) cout<<A[i];
}

Người ta nói tần số của một số A trong một dãy số A1, A2, …,An là số lần xuất hiện của số A trong dãy A1,A2,…,An.
Ví dụ: Cho dãy số 2 3 4 5 1 3 3 4 3
Tần số của số 2 là 1. Tần số của số 3 là 4.
Cho một file văn bản có tên TANSO.INP và có cấu trúc như sau:
Dòng 1: Chứa số nguyên N dương (0<N<=10000)
N dòng tiếp theo: mỗi dòng chứa một số nguyên Ai (0<Ai<101), các số ghi cách nhau ít nhất một dấu cách trống.
Hãy viết chương trình đọc file trên và tìm tần số xuất hiện của các số trong N số đã cho. Yêu cầu chương trình chạy không quá 2 giây.
Kết quả xuất ra file văn bản TANSO.OUT gồm nhiều dòng. Mỗi dòng chứa 2 số Ai và Ki ghi cách nhau ít nhất một dấu cách trống. Trong đó Ai là số thuộc dãy, Ki là tần số của số Ai. Ai được xếp tăng dần từ đầu đến cuối file.

Có 3 loại hình thức nhận thưởng: sách+sổ, sách+bút, sổ+bút
Gọi số học sinh nhận được phần thưởng thuộc 3 loại nói trên lần lượt là x;y;z
\(\Rightarrow\left\{{}\begin{matrix}x+y=9\\x+z=8\\y+z=11\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=3\\y=6\\z=5\end{matrix}\right.\)
Hay chúng ta có 3 bạn nhận thưởng sách+sổ, 6 bạn nhận sách+bút, 5 bạn nhận sổ+bút
Như vậy có 3 TH để An và Bình nhận thưởng giống nhau là:
- An Bình cùng nhận sách sổ: còn lại 12 bạn, chọn 6 bạn nhận sách bút có \(C_{12}^6\) sách, còn lại 6 bạn, chọn 5 bạn nhận sổ bút có \(C_6^5\) cách, còn 1 bạn, chọn 1 bạn nhận sách sổ có \(C_1^1\) cách \(\Rightarrow C_{12}^6.C_6^5.C_1^1\) cách
- An Bình nhận sách bút: tương tự như trên ta có \(C_{12}^3.C_9^4.C_5^5\) cách
- An Bình nhận bút sổ: \(C_{12}^3.C_9^6.C_3^3\) cách
Tổng: \(51744\) cách
Gọi a là số học sinh nhận được sách và sổ ; b là số học sinh nhận được sách và bút ; c là số học sinh nhận được sổ và bút. Ta có : \(a+b=9,a+c=8,b+c=11\)
Giải ra ta được \(a=3,b=6,c=5\)
Xét ba trường hợp sau : TH 1 : An và Bình cùng nhận được sách và sổ. Có 3 người cùng nhận được sách và sổ, trong đó có An và Bình. Vì vậy cần chọn ra 1 người trong só 12 học sinh để nhận sách và sổ suy ra có \(C_{12}^1\) cách chọn. Sau đó chọn ra 6 em trong số 11 học sinh còn lại để nhận sách và bút và 5 học sinh còn lại nhận sổ và bút. Vậy số kết quả trong TH này là: \(C_{12}^1.C^6_{12}\)
TH 2 : An và Bình cùng nhận được sách và bút. Lập luận tương tự TH 1 ta có số kết quả trong TH này là : \(C_{12}^4.C_8^3\)
TH 3 : An và Bình cùng nhận được sổ và bút. Số kết quả trong TH này là :\(C_{12}^3.C_9^3\). . Vậy có: \(C_{12}^1.C_{12}^6+C_{12}^4.C_8^3+C_{12}^3.C_9^3=51744\) cách phát phần thưởng thỏa mãn bài toán.
Đáp án: \(51744\)

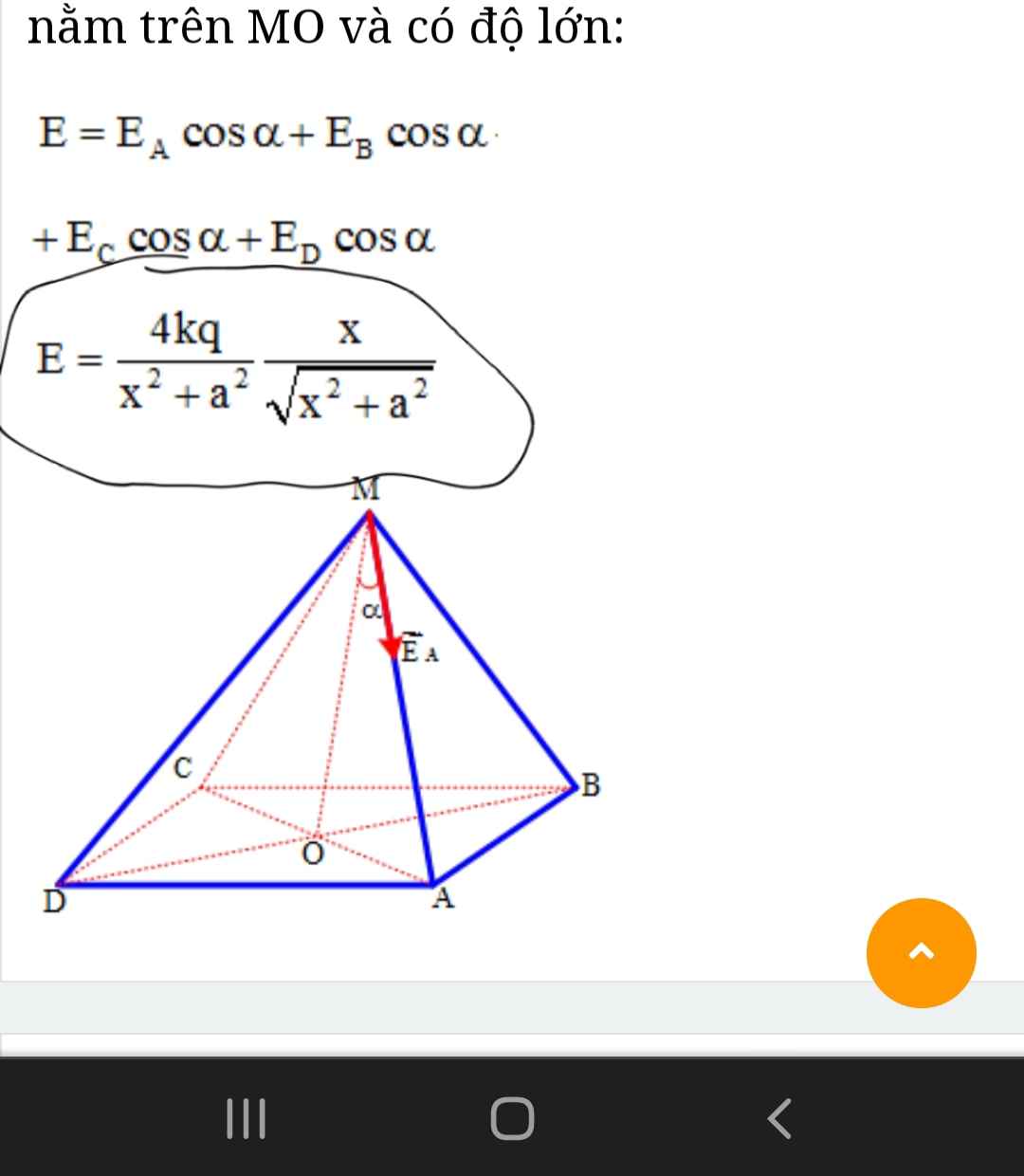
\(\dfrac{4kq.x}{\sqrt{\left(x^2+a^2\right)^3}}=\dfrac{4kq.x}{\sqrt{\left(x^2+\dfrac{a^2}{2}+\dfrac{a^2}{2}\right)^3}}\le\dfrac{4kq.x}{\sqrt{\dfrac{27.x^2.a^4}{4}}}=\dfrac{4kq.x}{\dfrac{3\sqrt{3}}{2}.x.a^2}=\dfrac{8\sqrt{3}.kq}{9a^2}\)
Dấu "=" xảy ra khi \(x=\dfrac{a}{\sqrt{2}}\)