Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 1 : Lập từng TH :
TH1 : Nếu x , y , z đều dương
suy ra ko thỏa mãn do xz = -9/13 (âm ) (S)
TH2 : Nếu x , y dương , z âm
suy ra ko thỏa mãn do yz = 3/7 ( dương ) (S)
TH3 : x âm , y,z dương
suy ra không thỏa mãn do xy = 2/5 (dương) (S)
TH4 : x , y , z đều am
suy ra không thỏa mãn do xz = -9/13 ( âm ) (S)
TH5 : x,y âm z dương
suy ra không thỏa mãn do yz = 3/7 ( dương ) (S)
Từ 5 trường hợp trên =) ko có số bố (x,y,z) thỏa mãn
Cách 2 :
Theo bài ra , ta có :
\(xy=\dfrac{2}{5},yz=\dfrac{3}{7},xz=-\dfrac{9}{13}\)
\(\Rightarrow xy.yz.xz=\dfrac{2}{5}\times\dfrac{3}{7}\times-\dfrac{9}{13}=-\dfrac{54}{455}\)
\(\Rightarrow\left(xyz\right)^2=-\dfrac{54}{455}\)
\(\Rightarrow xyz=\sqrt{\left(-\dfrac{54}{455}\right)}\)(Không xác định được vì một số bình phương không thể âm
Suy ra không có bộ (x,y,z) nào thỏa mãn các đk trên
Chúc bạn hok tốt =))![]()

a) Ta có : \(x - 2xy + y - 3 = 0\)
\(\Rightarrow-2xy+x+y=3\)
\(\Rightarrow-2.\left(-2xy+x+y\right)=-2.3\)
\(\Rightarrow4xy-2x-2y=-6\)
\(\Rightarrow4xy-2x-2y+1=-6+1\)
\(\Rightarrow2x.\left(2y-1\right).\left(2y-1\right)=-5\)
\(\Rightarrow\left(2y-1\right).\left(2x-1\right)=-5=1.\left(-5\right)=-5.1=\left(-1\right).5=5.\left(-1\right)\)
Tự lập bảng đi -.-
|
Nhân từng vế bất đẳng thức ta được : (xyz)2 = 36xyz + Nếu một trong các số x,y,z bằng 0 thì 2 số còn lại cũng bằng 0 + Nếu cả 3 số x,y,z khác 0 thì chia 2 vế cho xyz ta được xyz = 36 + Từ xyz =36 và xy = z ta được z2 = 36 nên z = 6; z = -6 + Từ xyz =36 và yz = 4x ta được 4x2 = 36 nên x = 3; x = -3 + Từ xyz =36 và ta được 9y2 = 36 nên y = 2; y = -2 - Nếu z = 6 thì x và y cùng dấu nên x = 3, y = 2 hoặc x = -3 , y = -2 - Nếu z = -6 thì x và y trái dấu nên x = 3 ; y = -2 hoặc x = -3; y=2 |
Vậy có 5 bộ số (x, y, z) thoã mãn: (0,0,0); (3,2,6);(-3,-2,6);(3,-2,-6);(-3,2.-6)

Ta có:
\(\left\{{}\begin{matrix}x^2+xy+\dfrac{y^2}{3}=2019\\z^2+\dfrac{y^2}{3}=1011\\x^2+xz+z^2=1008\end{matrix}\right.\Leftrightarrow x^2+xy+\dfrac{y^2}{3}=z^2+\dfrac{y^2}{3}+x^2+xz+z^2\)
\(\Rightarrow xy=2z^2+xz\Leftrightarrow xy+xz=2z^2+2xz\)
\(\Rightarrow x\left(y+z\right)=2z\left(x+z\right)\Leftrightarrow\dfrac{2z}{x}=\dfrac{y+z}{x+z}\left(đpcm\right)\)

Đặt \(\dfrac{x}{10}=\dfrac{y}{14}=\dfrac{z}{15}=k\)
⇔\(\left\{{}\begin{matrix}x=10k\\y=14k\\z=15k\end{matrix}\right.\)
Thay x = 10k; y = 14k và z = 15k vào xy + yz + xz = 2000 ta được :
140.k.k + 210.k.k + 150.k.k = 2000
⇔k.k .( 140 + 210 + 150 ) = 2000
\(\Leftrightarrow k^2\cdot500=2000\\ \Leftrightarrow k^2=4\\ \Leftrightarrow\left\{{}\begin{matrix}k=2\\k=-2\end{matrix}\right.\)
* Với k = 2, \(\Rightarrow\left\{{}\begin{matrix}x=20\\y=28\\z=30\end{matrix}\right.\)
*Với k = -2, \(\Rightarrow\left\{{}\begin{matrix}x=-20\\y=-28\\z=-30\end{matrix}\right.\)
Vậy ...................

1/ a, Ta có :
\(x-2y+3z=35\)
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}=\dfrac{x-2y+3z}{3-8+15}=\dfrac{35}{10}=\dfrac{7}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{7}{2}\Leftrightarrow x=\dfrac{21}{2}\\\dfrac{x}{4}=\dfrac{7}{2}\Leftrightarrow y=14\\\dfrac{z}{5}=\dfrac{7}{2}\Leftrightarrow z=\dfrac{35}{2}\end{matrix}\right.\)
Vậy ..
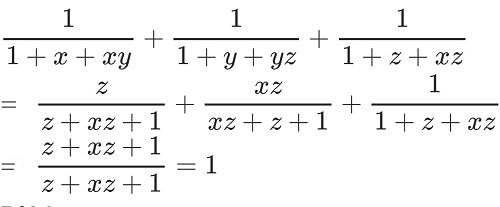
ta có:x.y.y.z.x.z=\(\dfrac{1}{2}.\dfrac{3}{5}.\dfrac{27}{10}=\dfrac{81}{100}\)
=>(x.y.z)2= \(\left(\dfrac{9}{10}\right)^2=\left(\dfrac{-9}{10}\right)^2\)
Nếu x.y.z=\(\dfrac{9}{10}\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{2}\\y=\dfrac{1}{3}\\z=\dfrac{9}{5}\end{matrix}\right.\)
Nếu x.y.z=\(\dfrac{-9}{10}\)
=>\(\left\{{}\begin{matrix}x=\dfrac{-3}{2}\\y=\dfrac{-1}{3}\\z=\dfrac{-9}{5}\end{matrix}\right.\)