Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có A = 5x2 - 2xy + 2y2 - 4x + 2y + 3
=> 2A = 10x2 - 4xy + 4y2 - 8x + 4y + 6
= (x2 - 4xy + 4y2) - 2(x - 2y) + 1 + 9x2 - 6x + 1 + 4
= \(\left(x-2y\right)^2-2\left(x-2y\right)+1+9\left(x^2-\frac{2}{3}x+\frac{1}{9}\right)+4\)
\(=\left(x-2y-1\right)^2+9\left(x-\frac{1}{3}\right)^2+4\)\(\ge4\)
=> A \(\ge\)2
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x-2y-=0\\x-\frac{1}{3}=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x-2y=1\\x=\frac{1}{3}\end{cases}}\Leftrightarrow\hept{\begin{cases}y=-\frac{1}{3}\\x=\frac{1}{3}\end{cases}}\)
Vậy khi x = 1/3 ; y = -1/3 thì A đạt GTNN
\(A=5x^2+2y^2-2xy-4x+2y\)\(+3\)
\(=\left(x^2-2xy+y^2\right)+\)\(\left(4x^2-4x+1\right)+\)\(\left(y^2+2y+1\right)+1\)
\(Tacó\)

=>5x^2+2y^2<2xy+4x+2y+1
=>5x^2+2y^2-2xy-4x-2y-1<0
=>x^2-2xy+y^2+4x^2-4x+1+y^2-2y+1<2
=>(x-y)^2+(2x-1)^2+(y-1)^2<2
=>2x-1=1 và y-1=0
=>y=1 và x=1

\(M=x^2+2y^2+2xy-2x-3y+1\)
=> \(M=x^2+2x\left(y-1\right)+\left(y-1\right)^2-\left(y-1\right)^2+2y^2-3y+1\)
=> \(M=\left(x+y-1\right)^2-y^2+2y-1+2y^2-3y+1\)
=> \(M=\left(x+y-1\right)^2+y^2-y\)
=> \(M=\left(x+y-1\right)^2+y^2-2y\frac{1}{2}+\frac{1}{4}-\frac{1}{4}\)
=> \(M=\left(x+y-1\right)^2+\left(y-\frac{1}{2}\right)^2-\frac{1}{4}\)
Có \(\left(x+y-1\right)^2\ge0\)với mọi x, y
\(\left(y-\frac{1}{2}\right)^2\ge0\)với mọi y
=> \(M=\left(x+y-1\right)^2+\left(y-\frac{1}{2}\right)^2-\frac{1}{4}\ge\frac{-1}{4}\)với mọi x, y
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+y-1=0\\y-\frac{1}{2}=0\end{cases}}\)
<=> \(\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{1}{2}\end{cases}}\)
KL: Mmin = \(\frac{-1}{4}\)<=> \(x=y=\frac{1}{2}\)

\(\sqrt{x+2}+x^3=y^3+\sqrt{y+2}\)
nếu x>y =>vt>vp
nếu x<y => vt<vp
nếu x=y => VT=VP
=> x=y
ta có\(M=-x^2+2x+2015=-\left(x-1\right)^2+2016\)
=>M max=2016<=>x=y=1

\(A=\sqrt{x^2-5x+10}=\sqrt{x^2-5x+\dfrac{25}{4}+\dfrac{15}{4}}=\sqrt{\left(x-\dfrac{5}{2}\right)^2+\dfrac{15}{4}}\ge\sqrt{\dfrac{15}{4}}\)
Vậy GTNN của A là \(\sqrt{\dfrac{15}{4}}\) . Dấu \("="\) xảy ra khi \(x=\dfrac{5}{2}\)
Ý B thì dễ nhưng giải ra thì ko phù hợp !
b) ta có : \(B\ge0\)
dâu "=" xảy ra khi \(2x^2-x-7=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1+\sqrt{57}}{4}\\x=\dfrac{1-\sqrt{57}}{4}\end{matrix}\right.\)
c) \(C=x^2+2y^2+2xy-2x+y=x^2+2xy+y^2+y^2+y+\dfrac{1}{4}-2x-\dfrac{1}{4}\)
\(C=\left(x+y\right)^2+\left(y+\dfrac{1}{2}\right)^2-2x-\dfrac{1}{4}\ge-2x-\dfrac{1}{4}\)
dâu "=" xảy ra khi \(x=y=\dfrac{-1}{2}\) thế ngược lại rồi kết luận

\(2xy\le x^2+y^2\)
\(\Rightarrow x^2+y^2+4x+2y+1>5x^2+2y^2\)
\(\Rightarrow4x^2-4x+1+y^2-2y+1< 3\)
\(\Rightarrow\left(2x-1\right)^2+\left(y-1\right)^2< 3\)
Do \(x\) nguyên \(\Rightarrow2x-1\ne0\), ta có các trường hợp xảy ra:
\(\left\{{}\begin{matrix}\left(2x-1\right)^2=1\\\left(y-1\right)^2=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\\y=1\end{matrix}\right.\)
\(\left\{{}\begin{matrix}\left(2x-1\right)^2=1\\\left(y-1\right)^2=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\\\left[{}\begin{matrix}y=0\\y=2\end{matrix}\right.\end{matrix}\right.\)
Thế ngược vào BPT ban đầu ta thấy chỉ có các cặp \(\left(x;y\right)=\left(0;1\right);\left(1;1\right);\left(0;0\right)\) là thỏa mãn
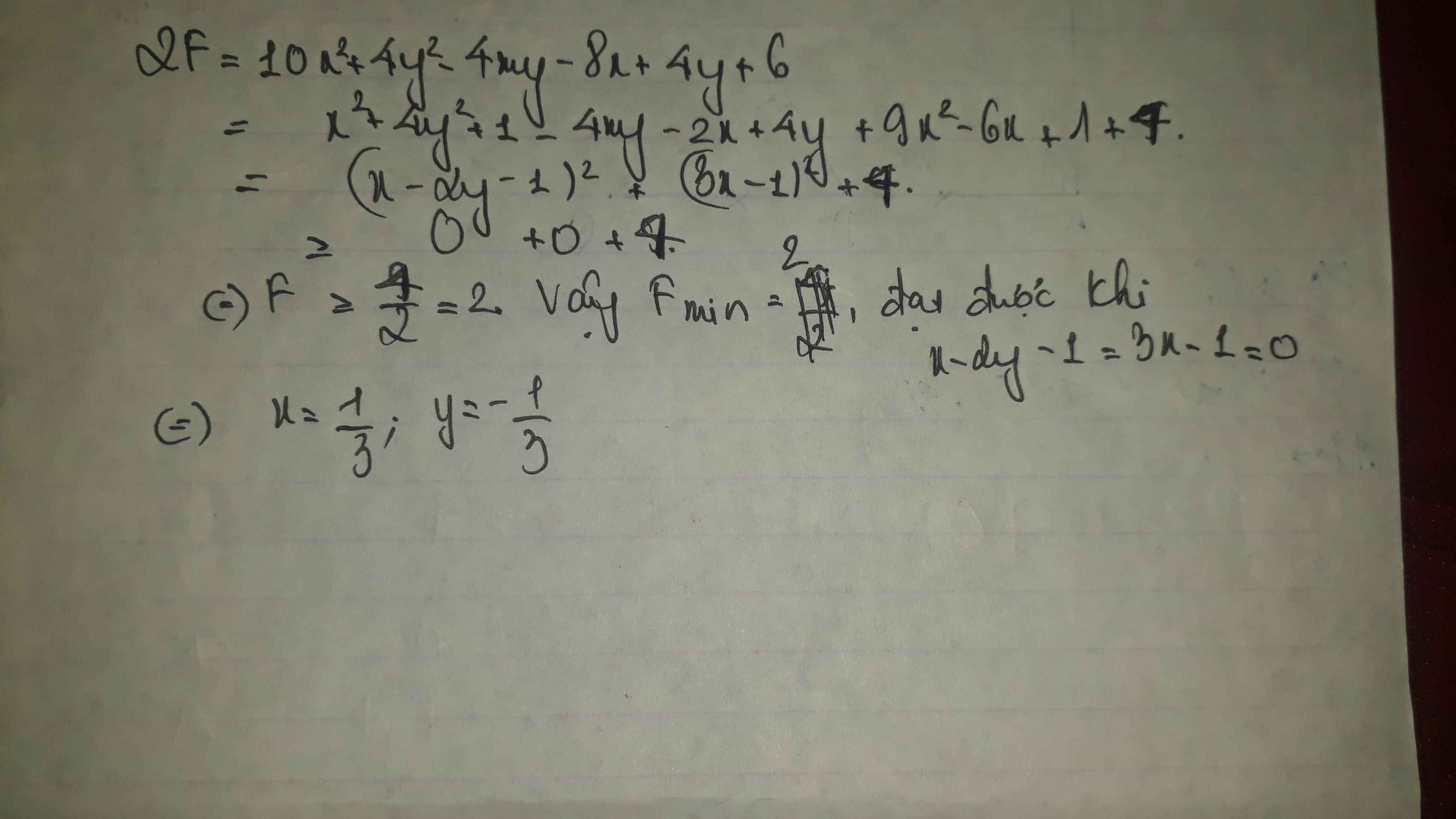
\(F=\frac{1}{9}\left(9x^2+9y^2+4-18xy-12x+12y\right)+\frac{4}{9}\left(9x^2-6x+1\right)+\frac{1}{9}\left(9y^2+6y+1\right)+2\)
\(F=\frac{1}{9}\left(3x-3y-2\right)^2+\frac{4}{9}\left(3x-1\right)^2+\frac{1}{9}\left(3y+1\right)^2+2\ge2\)
\(F_{min}=2\) khi \(\left\{{}\begin{matrix}x=\frac{1}{3}\\y=-\frac{1}{3}\end{matrix}\right.\)