
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


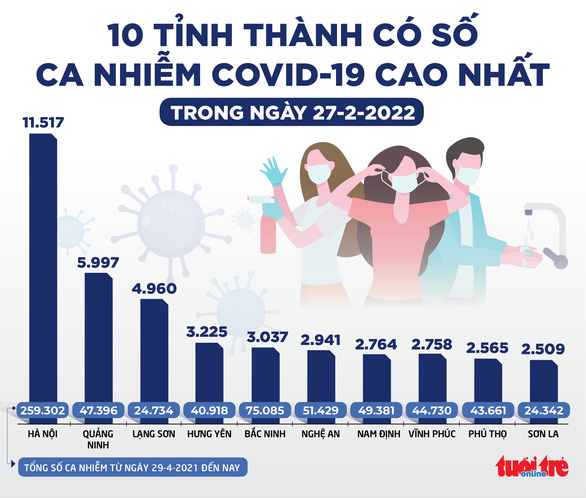
a. Những tỉnh thành phố có ca nhiễm hơn 2800 ca: Nghệ An, Bắc Ninh, Hưng Yên, Lạng Sơn, Quảng Ninh, Hà Nội.
b. Tỉnh có số ca nhiễm Covid 19 cao nhất là: Hà Nội

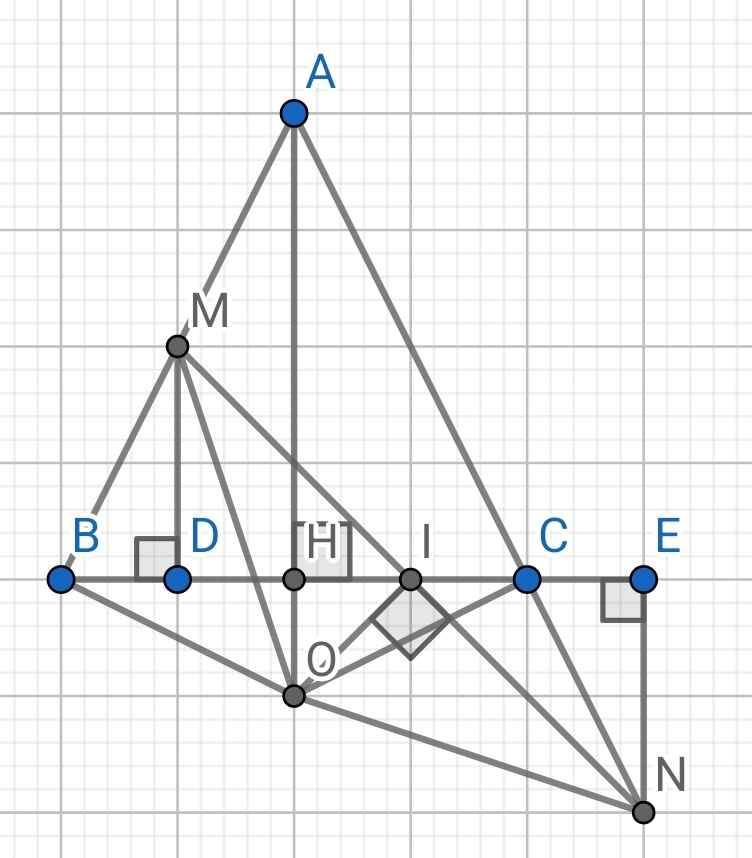 a) ∆ABC cân tại A
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC

 a) ∆ABC cân tại A
a) ∆ABC cân tại A
⇒ ∠ABC = ∠ACB
Mà ∠ACB = ∠ECN (đối đỉnh)
⇒ ∠ABC = ∠ECN
⇒ ∠DBM = ∠ECN
Xét hai tam giác vuông: ∆DBM và ∆ECN có:
BD = CE (gt)
∠DBM = ∠ECN (cmt)
⇒ ∆DBM = ∆ECN (cạnh góc vuông - góc nhọn kề)
⇒ DM = EN (hai cạnh tương ứng)
b) Do DM ⊥ BC (gt)
EN ⊥ BC (gt)
⇒ DM // EN
⇒ ∠DMI = ∠ENI (so le trong)
Xét hai tam giác vuông: ∆DMI và ∆ENI có:
DM = EN (cmt)
∠DMI = ∠ENI (cmt)
⇒ ∆DMI = ∆ENI (cạnh góc vuông - góc nhọn kề)
⇒ MI = NI (hai cạnh tương ứng)
⇒ I là trung điểm của MN
⇒ BC cắt MN tại trung điểm I của MN
c) Do AH ⊥ BC nên AH là đường cao của ∆ABC
Mà ∆ABC cân tại A
AH cũng là đường phân giác của ∆ABC
⇒ ∠BAH = ∠CAH
⇒ ∠BAO = ∠CAO
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆OAB và ∆OAC có:
OA là cạnh chung
∠BAO = ∠CAO (cmt)
AB = AC (cmt)
⇒ ∆OAB = ∆OAC (c-g-c)
⇒ OB = OC (hai cạnh tương ứng)
Ta có:
I là trung điểm MN (cmt)
OI ⊥ MN (gt)
⇒ OI là đường trung trực của MN
⇒ OM = ON
Do ∆DBM = ∆ECN (cmt)
⇒ BM = CN (hai cạnh tương ứng)
Xét ∆OBM và ∆OCN có:
OB = OC (cmt)
OM = ON (cmt)
BM = CN (cmt)
⇒ ∆OBM = ∆OCN (c-c-c)
d) Do ∆OBM = ∆OCN (cmt)
⇒ ∠OBM = ∠OCN (hai góc tương ứng)
Do ∆OAB = ∆OAC (cmt)
⇒ ∠OBA = ∠OCA (hai góc tương ứng)
⇒ ∠OBM = ∠OCA
Mà ∠OBM = ∠OCN (cmt)
⇒ ∠OCN = ∠OCA
Mà ∠OCN + ∠OCA = 180⁰ (kề bù)
⇒ ∠OCN = ∠OCA = 180⁰ : 2 = 90⁰
⇒ OC ⊥ AC

Lời giải:
Trên $AC$ lấy $E$ sao cho $AB=AE$. Xét tam giác $ABD$ và $AED$ có:
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là tia phân giác $\widehat{A}$)
$AD$ chung
$AB=AE$
$\Rightarrow \triangle ABD=\triangle AED$ (c.g.c)
$\Rightarrow BD=DE(1)$ và $\widehat{ABD}=\widehat{AED}$
Có:
$\widehat{DEC}=180^0-\widehat{AED}=180^0-\widehat{ABD}=\widehat{ECD}+\widehat{BAC}> \widehat{ECD}$
$\Rightarrow DC> DE(2)$
Từ $(1); (2)\Rightarrow DC> DB$

\(\widehat{M_1}\) = \(\widehat{M_3}\) (hai góc đối đỉnh)
\(\widehat{M_3}\) + \(\widehat{N_1}\) = 1800 (hai góc trong cùng phía)
\(\widehat{M_3}\) = 1800 - \(\widehat{N_1}\)
\(\widehat{M_3}\) = 1800 - 500
\(\widehat{M_3}\) = 1300
⇒ \(\widehat{M_1}\) = 1300
Kết luận: \(\widehat{M_1}\) = 1300

Bài 1:
Xét ΔBAK vuông tại A và ΔBHK vuông tại H có
BK chung
KA=KH
=>ΔBAK=ΔBHK
=>BA=BH
mà KA=KH
nên BK là trung trực của AH
=>BK vuông góc AH

Do tam giác MQE vuông tại E \(\Rightarrow\widehat{EMQ}+\widehat{EQM}=90^0\) (1)
Mà \(\widehat{EQM}\) là góc ngoài của tam giác NPQ, theo tính chất góc ngoài của tam giác:
\(\widehat{EQM}=\widehat{ENP}+\widehat{QPN}\) (2)
\(\left(1\right);\left(2\right)\Rightarrow\widehat{EMQ}+\widehat{ENP}+\widehat{QPN}=90^0\)
\(\Rightarrow\widehat{EMQ}+\widehat{ENP}+\widehat{QPN}-90^0=0\)






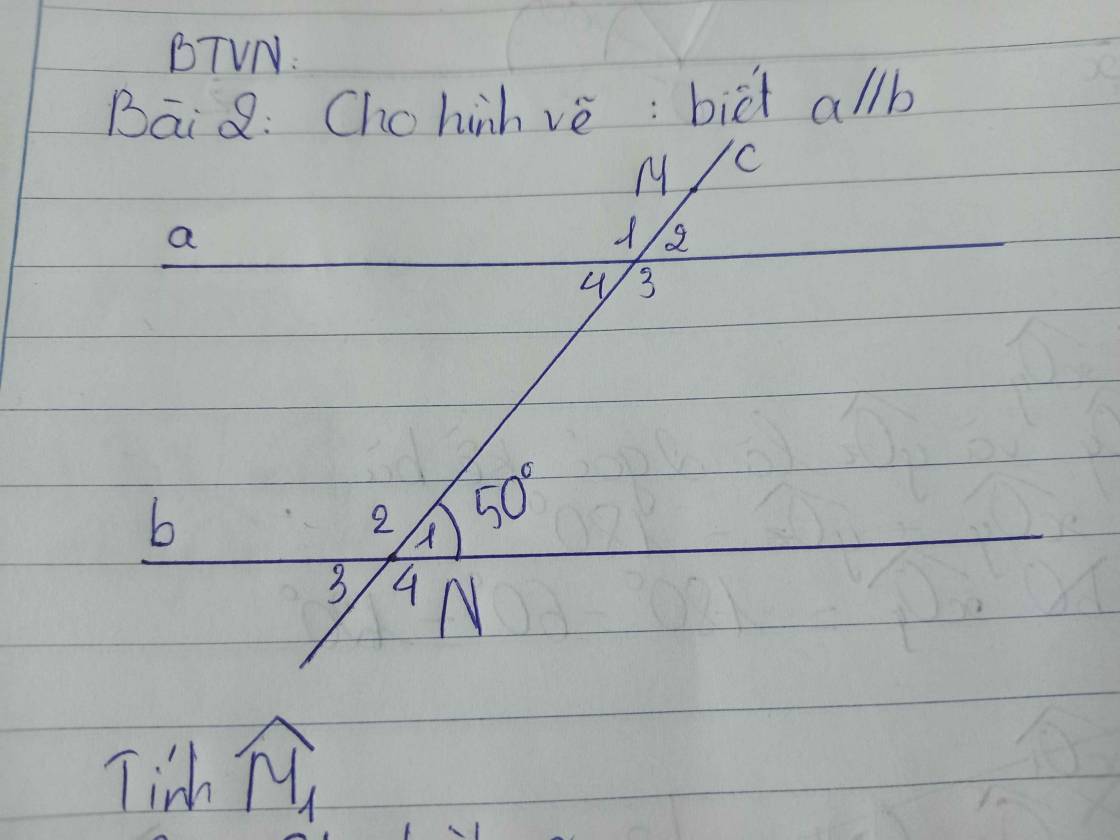

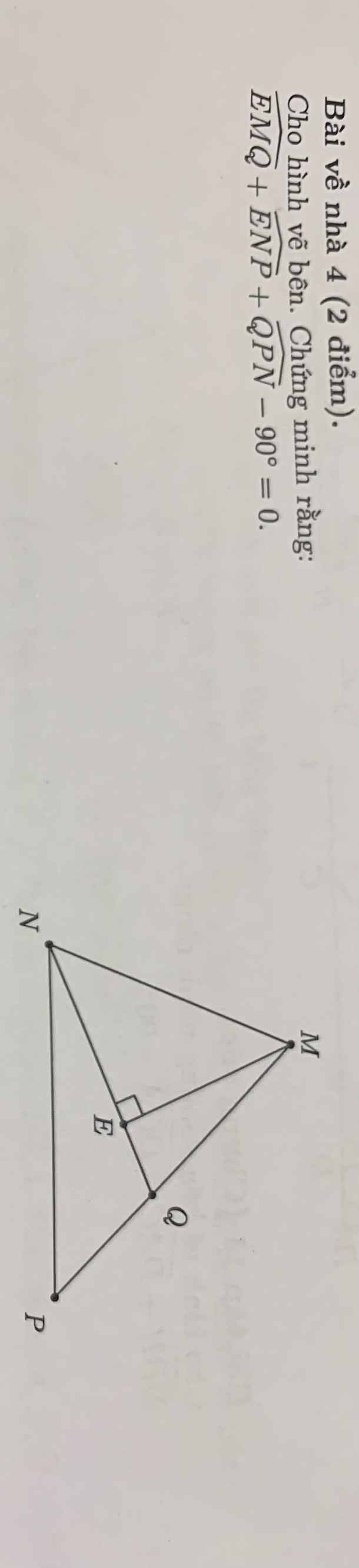
`x/y=5/7`
`=>x/5=y/7`
mà `x+y=36` nên áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{x}{5}=\dfrac{y}{7}=\dfrac{x+y}{5+7}=\dfrac{36}{12}=3\\ =>\dfrac{x}{5}=3=>x=3\cdot5=15\\ =>\dfrac{y}{7}=3=>y=3\cdot7=21\)
Ta có: `x/y=5/7 -> x/5=y/7`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/5=y/7=(x+y)/(5+7)=36/12=3`
`-> x/5=y/7=3`
`-> x=3*5=15, y=3*7=21`