Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\frac{1.2.3.4....30.31}{2.2.2.3.2.3.....2.32}=\frac{2.3.4....30.31}{2^{31}\left(2.3...31\right).32}=\frac{1}{2^{31}.2^5}=\frac{1}{2^{36}}=2^{-36}\)
Vậy x=-36
ta có \(\frac{1}{4}\cdot\frac{2}{6}\cdot\frac{3}{8}.....\frac{30}{62}\cdot\frac{31}{64}=2^x\)
=>\(\frac{1.2.3.4....31}{2\cdot2\cdot2\cdot3\cdot2\cdot3.....\cdot2\cdot3\cdot2}=\frac{2\cdot3\cdot4...30.31}{2^{31}\left(2\cdot3\cdot4...31\right)32}=\frac{1}{2^{31}\cdot2^5}=\frac{1}{2^{36}}=2^{-36}\)
\(=>x=-36\)

a)\(\left(x-1\right)^{x+2}=\left(x-1\right)^{x+4}\Leftrightarrow\left(x-1\right)^{x+2}\left[\left(x-1\right)^2-1\right]=0\Leftrightarrow x\left(x-1\right)^{x+2}\left(x-2\right)=0\)
Do đó \(x\in\left\{0;1;2\right\}\)
b)
\(\frac{1}{4}\cdot\frac{2}{6}\cdot\frac{3}{8}\cdot...\cdot\frac{31}{64}=2^x\Leftrightarrow\frac{1\cdot2\cdot3\cdot...\cdot31}{4\cdot6\cdot8\cdot...\cdot64}=2^x\Leftrightarrow\frac{31!}{\left(2\cdot2\right)\cdot\left(2\cdot3\right)\cdot\left(2\cdot4\right)\cdot...\cdot\left(2\cdot31\right)\cdot64}=2^x\)
\(\frac{31!}{2^{30}\cdot31!\cdot2^6}=2^x\Leftrightarrow\frac{1}{2^{36}}=2^x\Leftrightarrow2^{-36}=2^x\Rightarrow x=-36\)

a) \(14:\frac{0,4x+0,6}{x}=7\)
\(\frac{0,4x+0,6}{x}=2\)
0,4x + 0,6 = 2.x
2x - 0,4x = 0,6
1,6x = 0,6
x = 0,375
b) \(\left(160\%+\frac{2}{3}x-x\right).12=660\)
\(\left(160\%+\frac{2}{3}x-x\right)=55\)
\(x\left(\frac{2}{3}-1\right)=53,4\)
\(-\frac{1}{3}x=\frac{267}{5}\)
\(x=\frac{267}{5}.\frac{3}{-1}\)
\(x=-160,2\)
c) \(1:\frac{1.2.3.4.....31}{2.2.2.3.2.4.....2.32}=2^x\)
\(1:\frac{1.2.3.4.....31}{2^{31}.2.3.4.....31.2^5}=2^x\)
\(1:\frac{1}{2^{36}}=2^x\)
\(2^{36}=2^x\)
\(x=36\)

\(E=\frac{1\cdot2\cdot3\cdot4\cdot...\cdot30\cdot31}{4\cdot6\cdot8\cdot10\cdot...\cdot62\cdot64}=\frac{1\cdot1\cdot1\cdot1\cdot.....\cdot1\cdot1}{2\cdot2\cdot2\cdot....\cdot2\cdot64}=\frac{1}{2\cdot30\cdot64}=\frac{1}{3840}\)

\(\frac{4}{1}.\frac{6}{2}.\frac{8}{3}.\frac{10}{4}...\frac{64}{31}=\frac{2^{31}.\left(2.3.4.5...32\right)}{1.2.3.4...31}=2^{31}.32\)
Mà \(2^x=2^{31}.32=2^{31}.2^5=2^{36}\)
\(\Rightarrow x=36\)

a) \(\frac{1}{4}+\frac{3}{4}:x=\frac{5}{8}\)
\(\frac{3}{4}:x=\frac{3}{8}\)
\(x=2\)
vậy x=2
b) \(\frac{1}{3}+\frac{1}{6}+\frac{1}{10}+...+\frac{2}{x.\left(x+1\right)}=\frac{2000}{2002}\)
\(\frac{2}{6}+\frac{2}{12}+...+\frac{2}{x.\left(x+1\right)}=\frac{2000}{2002}\)
\(2.\left(\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{x.\left(x+1\right)}\right)=\frac{2000}{2002}\)
\(2.\left(\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{x}-\frac{1}{x+1}\right)=\frac{2000}{2002}\)
\(2.\left(\frac{1}{2}-\frac{1}{x+1}\right)=\frac{2000}{2002}\)
\(\frac{1}{2}-\frac{1}{x+1}=\frac{1000}{2002}\)
\(\frac{1}{x+1}=\frac{1}{2002}\)
\(x+1=2002\)
\(x=2001\)
vậy x=2001

\(=\frac{1x2x3x...x30x31}{2^{31}x\left(2x3x4x...x31x32\right)}=\frac{1}{2^{31}x32}=\frac{1}{2^{36}}\)
1/4 . 2/6 . 3/8 . ... .30/62 .31/64 = 2^x
(1/2 . 1/2).(2/3 . 1/2).(3/4 . 1/2). ... .(30/31 . 1/2).(31/32 . 1/2) = 2^x
(1/2.1/2. ... .1/2).(1/2 . 2/3 . 3/4. ... .30/31 . 31/32) = 2^x
(31 số 1/2)
(1/2)^31.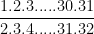 = 2^x
= 2^x
=> 0=x+36
x=0-36
x=-36
Vậy x=-36
Theo mk nghĩ,mk làm đúng nha .Tk cho mk
Để mk sửa phần này một chút
\((\frac{1}{2})^{31}\cdot\frac{1\cdot2\cdot3.....30\cdot31}{2\cdot3\cdot4.....31\cdot32}=2^x\)
\(\frac{1^{31}}{2^{31}}\cdot\frac{1}{32}=2^x\)
\(\frac{1}{2^{31}}\cdot\frac{1}{2^5}=2^x\)
\(\frac{1}{2^{36}}=2^x\)
\(1=2^x\cdot2^{36}\)
\(2^0=2^x+36\)
Rồi bn tự suy luận nha