Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Các tia Om, On tương ứng là tia phân giác của góc yOz và xOz vì:
Tia Om nằm trong góc yOz và \(\widehat {yOm} = \widehat {mOz}\)
Tia On nằm trong góc xOz và \(\widehat {xOn} = \widehat {nOz}\)
b) Vì các tia Om, On tương ứng là tia phân giác của góc yOz và xOz nên: \(\widehat {yOm} = \widehat {mOz} = \frac{1}{2}.\widehat {yOz};\widehat {xOn} = \widehat {nOz} = \frac{1}{2}.\widehat {xOz}\)
Mà tia Oz nằm trong góc xOy nên \(\widehat {yOz} + \widehat {xOz} = \widehat {xOy}\)
\( \Rightarrow \widehat {mOz} + \widehat {zOn} = \frac{1}{2}.\widehat {yOz} + \frac{1}{2}.\widehat {xOz} = \frac{1}{2}.\widehat {xOy}\)
Mà tia Oz nằm trong góc mOn nên \(\widehat {mOz} + \widehat {zOn} = \widehat {mOn}\) và \(\widehat {xOy} = 90^\circ \)
\( \Rightarrow \widehat {mOn} = \frac{1}{2}.90^\circ = 45^\circ \)

a) Hai góc \(\widehat {xOy}\) và \(\widehat {yOz}\) có cạnh Oy chung, không có điểm trong chung
b) Ta có:
\(\begin{array}{l}\widehat {xOy} = 30^\circ ,\widehat {yOz} = 45^\circ ,\widehat {xOz} = 75^\circ \\ \Rightarrow \widehat {xOy} + \widehat {yOz} = \widehat {xOz}\end{array}\)
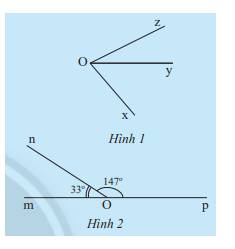
c) Ta có: \(\widehat {mOn} + \widehat {nOp} = 33^\circ + 147^\circ = 180^\circ \)

1: Xét ΔOIA vuông tại I và ΔOIB vuông tại I có
OI chung
IA=IB
=>ΔOIA=ΔOIB
=>OA=OB
=>ΔOAB cân tại O
2: OA+AM=OM
OB+BN=ON
mà OA=OB và AM=BN
nên OM=ON
=>ΔOMN cân tại O
Xét ΔOMN có OA/OM=OB/ON
nên AB//MN

xOy + tOx = 180o ( kề bù)
xOy + yOz = 180o ( kề bù)
mà xOy = xOy.
=> 2 góc này bằng nhau ( 2 góc cùng kề bù với góc thứ 3 thì bằng nhau).
=> 2 góc đối đỉnh.
like và tim bạn nhé

Om là phân giác góc xOy
=> góc mOy = 1/2 góc xOy
On là phân giác góc yOz
=> góc yOn = 1/2 góc yoz
suy ra: góc mOy + góc yOn = 1/2 (góc xOy + góc yOz)
<=> góc mOn = 1/2.1800 = 900 (do góc xOy và góc yOz kề bù)
Om phân giác xoy => moy=1/2xoy hay xoy=2moy
tương tự => noy=1/2yoz hay yoz=2noy
Lại có:
xoy+yoz=180
=>2moy +2noy=180
=>moy+noy=90 hay mon =90

a) +) Vì Ox đối với Ox' và Oy đối với Oy' nên \(\widehat{xOy}\) và \(\widehat{x'Oy'}\) đối đỉnh
\(\Rightarrow\)\(\widehat{xOy}=\)\(\widehat{x'Oy'}\)
hay \(\widehat{x'Oy'}\)\(=40^0\)
+) Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\) (kề bù)
hay \(40^0+\widehat{x'Oy}=180^0\)
\(\Leftrightarrow\widehat{x'Oy}=180^0-40^0\)
\(\Leftrightarrow\widehat{x'Oy}=140^0\)
+) Ta có: \(\widehat{xOy}+\widehat{xOy'}=180^0\) (kề bù)
hay \(40^0+\widehat{xOy'}=180^0\)
\(\Leftrightarrow\widehat{xOy'}=180^0-40^0\)
\(\Leftrightarrow\widehat{xOy'}=140^0\)
b) Vì \(\widehat{xOy}=\widehat{x'Oy'}\)(hai góc đối đỉnh)
Mà Om là tia phân giác của góc xOy và On là tia phân giác của x'Oy' nên Om đối On (đpcm)
a, Vì góc x'Oy' và góc xOy là hai góc đối đỉnh, mà \(\widehat{xOy}=40^0\)nên \(\widehat{x'Oy'}=40^0\). Góc xOy và góc xOy' là hai góc kề bù nên \(\widehat{xOy}+\widehat{xOy'}=180^0\)hay \(40^0+\widehat{xOy'}=180^0\)
=> \(\widehat{xOy'}=180^0-40^0=140^0\)
Góc xOy' là góc đối đỉnh với góc xOy' nên \(\widehat{xOy}=\widehat{x'Oy}=140^0\)
b, Om,On theo thứ tự là các tia phân giác của hai góc xOy và x'Oy' nên \(\widehat{xOm}=\widehat{mOy}=\frac{1}{2}\widehat{xOy}\)và \(\widehat{nOx'}=\widehat{mOy'}=\frac{1}{2}\widehat{x'Oy'}\)mà \(\widehat{xOy}=\widehat{x'Oy'}\), do đó \(\widehat{xOm}=\widehat{mOy}=\widehat{nOx'}=\widehat{nOy'}=\frac{1}{2}\widehat{xOy}\).
Ta có : \(\widehat{xOm}=\widehat{nOy'}=\widehat{y'Ox}=\widehat{xOm}=\widehat{y'Ox}+\widehat{xOm}+\widehat{mOy}\)
\(=\widehat{y'Ox}+\widehat{xOy}=180^0\)
Góc mOn là góc bẹt,vì thế hai tia Om,On là hai tia đối nhau

`Answer:`
Ta có `hat{zOt}+\hat{yOz}=90^o`
\(\Rightarrow\frac{1}{2}.Oz+\widehat{yOz}=90^o\)
\(\Rightarrow\frac{1}{2}.4\widehat{yOz}+\widehat{yOz}=90^o\)
\(\Rightarrow\widehat{yOz}.3=90^o\)
\(\Rightarrow\widehat{yOz}=30^o\)
`=>\hat{xOz}=120^o` (Vì `\hat{xOz}=4\hat{yOz}`
Vậy `\hat{xOy}=\hat{yOz}+\hat{xOz}=120^o+30^o=150^o`


Chỉ mình với!
Bài làm
a) Vì \(\widehat{xOy}\)và \(\widehat{yOz}\)là hai góc kề bù
=> \(\widehat{xOy}+\widehat{yOz}=180^o\)
hay 50o + \(\widehat{yOz}\)= 180o
=> \(\widehat{yOz}\) = 180o - 50o
=> \(\widehat{yOz}\) = 130o
Vậy \(\widehat{yOz}\)= 130o
b) - Vì Om là tia phân giác của \(\widehat{xOy}\)
=> \(\widehat{mOy}=\frac{\widehat{xOy}}{2}=\frac{50^o}{2}=25^o\)(1)
- Vì On là tia phân giác của \(\widehat{yOz}\)
=> \(\widehat{yOn}=\widehat{\frac{yOz}{2}}=\frac{130^o}{2}=65^o\)(2)
Từ (1) và (2) => \(\widehat{mOy}+\widehat{yOn}=\widehat{mOn}\)
hay 25o + 65o = \(\widehat{mOn}\)
=> \(\widehat{mOn}\) = 25o+65o
=> \(\widehat{mOn}\) = 90o
Mà góc vuông có số đo bằng 90o
=> Om\(\perp\)On