Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
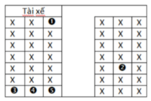
Số cách để xếp 8 người vào bàn tròn là: 7!=5040
Để xếp sao cho hai nữ không ngồi cạnh nhau trước tiên ta xếp 5 nam trước: 4!=24
Giữa 5 nam có 5 chỗ trống, số cách để xếp 3 nữ vào 5 chỗ trống: ![]()
Vậy xác suất để xếp sao cho hai nữ không ngồi cạnh nhau là: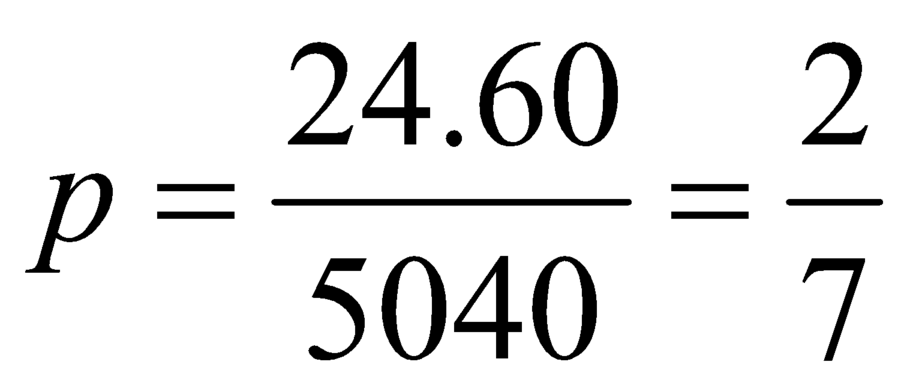

Số cách xếp quanh bàn tròn là \(n\left(\Omega\right)=9!\)
Kí hiệu A là biến cố : "Nam nữ ngồi xen kẽ nhau"
Ta có :
\(n\left(A\right)=4!5!\) và \(P\left(A\right)=\dfrac{4!5!}{9!}\approx0,008\)

Chọn D
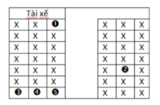
Gọi A là biến cố “ Xếp 7 người sao cho đứa trẻ ngồi giữa hai người đàn ông”
Ta có: ![]()
Xếp thỏa mãn đề bài theo các bước sau:
+Cố định đứa trẻ vào 1 ghế.
+Vì đứa trẻ ngồi giữa 2 người đàn ông nên xếp 2 người đàn ông ngồi bên cạnh đứa trẻ
có: A 4 2 (cách)
+Xếp 2 người đàn ông còn lại và 2 người đàn bà vào 4 ghế còn lại có: 4! (cách)
![]()
Vậy 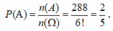

Chọn B
Số cách xếp ngẫu nhiên là 5! cách.
Ta tìm số cách xếp thoả mãn:
+ Chọn 2 vị trí cạnh nhau (3,4) và (4,5) có 2 cách.
+ Xếp A và B vào 2 vị trí cạnh nhau vừa chọn có 2! cách.
+ Xếp 3 người còn lại có 3! cách.
Số cách xếp là 2.2!3!. Xác suất cần tính bằng 

Đáp án B
Số phần tử KGM là: 9!. Mà số phần tử của biến cố các học sinh nữ luôn ngồi cạnh nhau là: 3!7!
Xác suất để các học sinh nữ luôn ngồi cạnh nhau là: 3 ! 7 ! 9 ! = 1 12