K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 1 2021
Ta có: \(x^3-7x-6=0\)
\(\Leftrightarrow x^3-x-6x-6=0\)
\(\Leftrightarrow x\left(x^2-1\right)-6\left(x+1\right)=0\)
\(\Leftrightarrow x\left(x-1\right)\left(x+1\right)-6\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[x\left(x-1\right)-6\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-x-6\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-3x+2x-6\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left[x\left(x-3\right)+2\left(x-3\right)\right]=0\)
\(\Leftrightarrow\left(x+1\right)\left(x+2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x+2=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-2\\x=3\end{matrix}\right.\)
Vậy: \(x\in\left\{-1;-2;3\right\}\)
SN
9 tháng 11 2016
\(x^6-7x^3-8=0\)
\(x^6-7x^3\) \(=0+8\)
\(x^6-7x^3\) \(=8\)
\(x^6-7x^3\) \(=2^3\)
\(x^6-7x\) \(=2\)
mk làm đến đây thui nha chỗ sau bn tự làm nha@@
17 tháng 10 2019
\(5x^2+7x-6=0\)
\(5x^2-10x+3x-6=0\)
\(5x\left(x-2\right)+3\left(x-2\right)=0\)
\(\left(x-2\right)\left(5x+3\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-2=0\\5x+3=0\end{cases}\Rightarrow\orbr{\begin{cases}x=2\\5x=-3\end{cases}\Rightarrow}\orbr{\begin{cases}x=2\\x=-\frac{3}{5}\end{cases}}}\)
KN
17 tháng 10 2019
\(5x^2+7x-6=0\)
Ta có: \(\Delta=7^2+4.5.6=169,\sqrt{\Delta}=13\)
Vậy pt có 2 nghiệm phân biệt:
\(x_1=\frac{-7+13}{10}=\frac{3}{5}\)'\(x_1=\frac{-7-13}{10}=-2\)
7 tháng 1 2022
\(\Leftrightarrow x^3+2x^2+2x^2+4x+3x+6=0\)
=>x+2=0
hay x=-2
12 tháng 9 2016
\(x^3-7x-6=0\)
\(\Leftrightarrow x^3+x^2-x^2-6x-x-6=0\)
\(\Leftrightarrow\left(x^3+x^2\right)-\left(x^2+x\right)-\left(6x+6\right)=0\)
\(\Leftrightarrow x^2\left(x+1\right)-x\left(x+1\right)-6\left(x+1\right)=0\)
\(\Leftrightarrow\left(x^2-x-6\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[x\left(x-3\right)+2\left(x-3\right)\right]\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-3\right)\left(x+1\right)=0\)
\(\left[\begin{array}{nghiempt}x+2=0\\x-3=0\\x+1=0\end{array}\right.\Leftrightarrow\left[\begin{array}{nghiempt}x=-2\\x=3\\x=-1\end{array}\right.\)
Vây ...................
2 tháng 8 2016
x^3 - 4x - 3x - 6 =0
\(\Leftrightarrow\)x(x^2-4) - 3(x+2) =0
\(\Leftrightarrow\)x(x-2)(x+2) - 3(x+2)=0
\(\Leftrightarrow\)(x+2)(x^2-2x-3)=0
\(\Leftrightarrow\)(x+2)(x^2-3x+x-3)=0
\(\Leftrightarrow\)(x+2)(x+1)(x-3)=0
\(\Leftrightarrow\)x=3 hoặc x=-1 hoặc x=-3
2 tháng 8 2016
Gọi \(A\) = \(x^3-7x-6\)
\(A=x^3-x^2+x^2-x-6x+6\)
\(A=x^2\left(x-1\right)+x\left(x-1\right)-6\left(x-1\right)\)
\(A=\left(x-1\right)\left(x^2+x-6\right)\)
\(A=\left(x-1\right)\left(x^2+3x-2x-6\right)\)
\(A=\left(x-1\right)\left[x\left(x+3\right)-2\left(x+3\right)\right]\)
\(A=\left(x-1\right)\left(x+3\right)\left(x-2\right)\)
VL
1
NG
20 tháng 5 2022
|9x−8|+|7x−6|+|5x−4|+|3x−2|+x=0(1)|9x−8|+|7x−6|+|5x−4|+|3x−2|+x=0(1).
Vì |9x−8|+|7x−6|+|5x−4|+|3x−2|>0∀x|9x−8|+|7x−6|+|5x−4|+|3x−2|>0∀x
Nên từ (1) ⇒x<0⇒9x−8;7x−6;5x−4;3x−2<0⇒x<0⇒9x−8;7x−6;5x−4;3x−2<0.
Phương trình (1) trở thành:
8−9x+6−7x+4−5x+2−3x+x=0⇔20−23x=0⇔x=20/23>0(ktm)
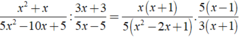
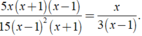
\(5x^2+7x-6=0\)
\(\Leftrightarrow5x^2-3x+10x-6=0\)
\(\Leftrightarrow x\left(5x-3\right)+2\left(5x-3\right)=0\)
\(\Leftrightarrow\left(5x-3\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}5x-3=0\\x+2=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{3}{5}\\x=-2\end{cases}}\)
Vậy ...
\(5x^2+7x-6=0\)
\(\Leftrightarrow5x^2-3x+10x-6=0\)
\(\Leftrightarrow\left(5x^2+3x\right)+\left(10x-6\right)=0\)
\(\Leftrightarrow x\left(5x-3\right)+2\left(5x-3\right)=0\)
\(\Leftrightarrow\left(5x-3\right)\left(x+2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}5x-3=0\\x+2=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{5}\\x=-2\end{cases}}}\)