HT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 8 2017
\(3x=4y;2y=5z\)
\(\Rightarrow\dfrac{x}{4}=\dfrac{y}{3};\dfrac{y}{5}=\dfrac{z}{2}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{15};\dfrac{y}{15}=\dfrac{z}{6}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}\)
\(\Rightarrow\dfrac{2x}{40}=\dfrac{3y}{45}=\dfrac{5z}{30}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{2x}{40}=\dfrac{3y}{45}=\dfrac{5z}{30}\)
\(=\dfrac{2x+3y-5z}{40+45-30}=\dfrac{55}{55}=1\)
\(\Rightarrow\left\{{}\begin{matrix}x=1.20=20\\y=1.15=15\\z=1.6=6\end{matrix}\right.\)
Tương tự
5 tháng 8 2017
Ta có :
\(2x+3y-5z=55\)
\(3x=4y;2y=5z\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{4};\dfrac{y}{2}=\dfrac{z}{5}\)
\(\Leftrightarrow\dfrac{x}{9}=\dfrac{y}{12};\dfrac{y}{12}=\dfrac{z}{16}\)
\(\Leftrightarrow\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{16}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{9}=\dfrac{y}{12}=\dfrac{z}{16}=\dfrac{2x+3y-5z}{2.19+3.12-2.16}=\dfrac{55}{22}=\dfrac{5}{2}\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{9}=\dfrac{5}{2}\Leftrightarrow x=\dfrac{45}{2}\\\dfrac{y}{12}=\dfrac{5}{2}\Leftrightarrow x=30\\\dfrac{z}{16}=\dfrac{5}{2}\Leftrightarrow z=40\end{matrix}\right.\)
Vậy ..............
30 tháng 10 2016
\(3x=2y;4y=5z\)
\(\Rightarrow\frac{x}{2}=\frac{y}{3};\frac{y}{5}=\frac{z}{4}\)
\(\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{x}{10}=\frac{y}{15};\frac{y}{5}=\frac{z}{4}\Rightarrow\frac{y}{15}=\frac{z}{12}\)
\(\frac{x}{10}=\frac{y}{15}=\frac{z}{12}\Rightarrow\)\(\frac{2x}{20}=\frac{3y}{45}=\frac{5z}{60}=\frac{2x-3y+5z}{125}=\frac{21}{125}\)
\(\frac{2x}{20}=\frac{21}{125}.....................\)
\(\frac{3y}{45}=\frac{21}{125}......................\)
........................................................................................................................................................................................................................................................................................................................................................
13 tháng 12 2021
\(\Leftrightarrow\dfrac{x}{4}=\dfrac{y}{3};\dfrac{y}{5}=\dfrac{z}{2}\\ \Leftrightarrow\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{6}=\dfrac{2x+3y-5z}{40+45-30}=\dfrac{55}{55}=1\\ \Leftrightarrow\left\{{}\begin{matrix}x=20\\y=15\\z=6\end{matrix}\right.\)
BT
1
14 tháng 9 2019
\(\frac{x}{4}=\frac{y}{3};3y=5z\) và x + y + z = 75
Ta có: \(\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\3y=5z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\\frac{y}{5}=\frac{z}{3}\end{cases}}\)
=> \(\frac{x}{4}=\frac{y}{3};\frac{y}{5}=\frac{z}{3}\)
=> \(\frac{x}{20}=\frac{y}{15};\frac{y}{15}=\frac{z}{9}\)
=> \(\frac{x}{20}=\frac{y}{15}=\frac{z}{9}\)
Áp dụng t/c dãy tỉ số bằng nhau ta có :
\(\frac{x}{20}=\frac{y}{15}=\frac{z}{9}=\frac{x+y+z}{20+15+9}=\frac{75}{44}\)
=> \(\hept{\begin{cases}\frac{x}{20}=\frac{75}{44}\\\frac{y}{15}=\frac{75}{44}\\\frac{z}{9}=\frac{75}{44}\end{cases}\Leftrightarrow}\hept{\begin{cases}x=\frac{375}{11}\\y=\frac{1125}{44}\\z=\frac{675}{44}\end{cases}}\)
\(3x=4y;2y=5z\)và x + y - z = 58
Ta có : \(\hept{\begin{cases}3x=4y\\2y=5z\end{cases}}\Rightarrow\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\\\frac{y}{5}=\frac{z}{2}\end{cases}}\)
=> \(\frac{x}{4}=\frac{y}{3};\frac{y}{5}=\frac{z}{2}\)
Từ \(\hept{\begin{cases}\frac{x}{4}=\frac{y}{3}\Rightarrow\frac{x}{20}=\frac{y}{15}\\\frac{y}{5}=\frac{z}{2}\Rightarrow\frac{y}{15}=\frac{z}{6}\end{cases}\Rightarrow\frac{x}{20}=\frac{y}{15}=\frac{z}{6}=\frac{x+y-z}{20+15-6}=\frac{58}{29}=2}\)
=> \(\hept{\begin{cases}\frac{x}{20}=2\\\frac{y}{15}=2\\\frac{z}{6}=2\end{cases}}\Rightarrow\hept{\begin{cases}x=40\\y=30\\z=12\end{cases}}\)
G
5 tháng 10 2018
Mình làm một câu để bạn tham khảo, sau đó bạn áp dụng làm các bài còn lại nha ^^
Có gì không hiểu bạn ib nha ^^
1. \(2x=3y-2x\left(1\right)\) và \(x+y=14\)
\(\left(1\right)\Leftrightarrow4x=3y\)
\(\Leftrightarrow\dfrac{x}{3}=\dfrac{y}{4}\)
Theo tính chất dãy tỉ số bằng nhau, có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{x+y}{3+4}=\dfrac{14}{7}=2\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2.3=6\\y=2.4=8\end{matrix}\right.\)
Bạn tự kết luận ^^
26 tháng 7 2021
a, Ta có : \(x:y:z=5:3:4\Rightarrow\frac{x}{5}=\frac{y}{3}=\frac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{5}=\frac{y}{3}=\frac{z}{4}=\frac{x+2y-z}{5+6-4}=-\frac{126}{7}=-18\)
\(x=-90;y=-54;z=-72\)
26 tháng 7 2021
b, \(5x=2y;3y=5z\Rightarrow\frac{x}{2}=\frac{y}{5};\frac{y}{5}=\frac{z}{3}\Rightarrow\frac{x}{2}=\frac{y}{5}=\frac{z}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{2}=\frac{y}{5}=\frac{z}{3}=\frac{x+y+z}{2+5+3}=-\frac{970}{10}=-97\)
\(x=-194;y=-485;z=-291\)
TN
2
9 tháng 8 2016
Theo đề bài, ta có:
\(3x=4y;3y=4z\) hay \(\frac{x}{3}=\frac{y}{4};\frac{y}{3}=\frac{z}{4}\) và 2x+3y-5z=55
\(\Rightarrow\frac{x}{9}=\frac{y}{12};\frac{y}{12}=\frac{z}{16}\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{9}=\frac{y}{12}=\frac{z}{16}=\frac{2x+3y-2z}{2.9+3.12-2.16}=\frac{55}{22}=\frac{5}{2}\)
- \(\frac{x}{9}=\frac{5}{2}.9=\frac{45}{2}\)
- \(\frac{y}{12}=\frac{5}{2}.12=30\)
- \(\frac{z}{16}=\frac{5}{2}.16=40\)
Vậy \(x=\frac{45}{2},y=30,z=40\)
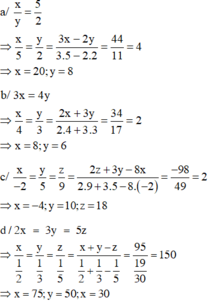
tick đúng cho ng` ta đi
mình cũng đang hắc búa bài này lắm, ai giải đc thì giải hộ tui vs nha. cái đồ k bt làm lại còn bảo k đúng để làm chó à, bực người. đã đang k làm đc toán sẵn gặp con này chắc tui chết mất