
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sin\widehat{B}=\dfrac{AC}{BC}\Rightarrow BC=\dfrac{AC}{\sin\widehat{B}}=\dfrac{4}{\sin42^o}\)
\(AC^2=CH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow CH=\dfrac{AC^2}{BC}=4.\sin42^o\)
Xét tg vuông AHC có
\(x=AH=\sqrt{AC^2-CH^2}\) (Pitago)
\(\Rightarrow x=\sqrt{16-16\sin^242^o}=4\sqrt{1-\sin^242}=4\sqrt{\cos^242^o}=4\cos42^o\)

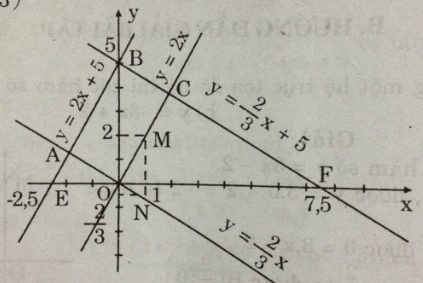
b)Bốn đường thẳng đã cho cắt nhau tại các điểm O, A.
Vì đường thẳng y = 2x + 5 song song với đường thẳng y = 2x, đường thẳng y = - 2x/3 +5 song song với đường thẳng y = - 2x/3 , tứ giác OABC là hình bình hành (có hai cặp cạnh song song).
Vậy tứ giác OABC là hình bình hành

Bạn tự vẽ nha
Mà câu a vs b cũng ko cần có cái ĐK đâu
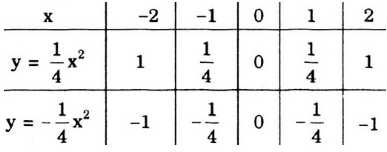
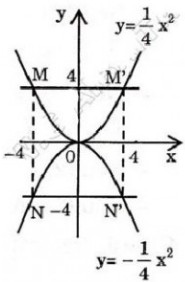
a) Đồ thị hàm số \(y=-x^2\) là một đường thẳng đi qua 2 điểm A\(\left(1;-1\right)\) và B\(\left(2;-2\right)\) (có thể đặt các hệ số khác tùy thích)
b) Đồ thị hàm số \(y=2x^2\) là một đường thẳng đi qua 2 điểm C\(\left(1;2\right)\) và D\(\left(2;8\right)\)
c) Ta có: \(y=-x.\left|x\right|\)
Có 2 trường hợp:
Với \(x\ge0\) thì \(y=-x.x\) \(\Leftrightarrow\) \(y=-x^2\) (là câu a)
Với \(x\le0\) thì \(y=-x.-x\) \(\Leftrightarrow\) \(y=x^2\)
Rồi bạn vẽ 2 cái đồ thị của 2 hàm số vừa tìm đc

bn lên mạng hoặc vào câu hỏi tương tự nha!
chúc bn hok tốt!
hahaha!
#conmeo#

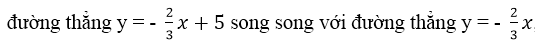


Xét tg vuông ABH và tg vuông ACH có
\(\widehat{BAH}=\widehat{ACH}\) (cùng phụ với \(\widehat{ABC}\) )
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{BH}{AH}\Rightarrow\dfrac{BH}{30}=\dfrac{5}{6}\Rightarrow BH=25\)
Ta có
\(AH^2=BH.CH\) (trong tg vuông bình phương đường cao hạ từ đỉnh góc vuông bằng tích giữa hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow CH=\dfrac{AH^2}{BH}=\dfrac{30^2}{25}=36\)
=> x=25; y=36