K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
2
17 tháng 5 2016
a) \(xy+3x-2y-11=0\)
\(x\left(y+3\right)-2y-6-5=0\)
\(x\left(y+3\right)-2\left(y+3\right)=5\)
\(\left(x-2\right)\left(y+3\right)=5\)
\(x-2;y+3\in U\left(5\right)\)
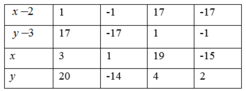
| x-2 | 1 | -1 | 5 | -5 |
| y+3 | 5 | -5 | 1 | -1 |
| x | 3 | 1 | 7 | -3 |
| y | 2 | -8 | -2 | -4 |
b) \(xy+2x+y+11=0\)
\(x\left(y+2\right)+y+2+9=0\)
\(x\left(y+2\right)+\left(y+2\right)=-9\)
\(\left(x+1\right)\left(y+2\right)=-9\)
\(x+1;y+2\in U\left(-9\right)\)
| x+1 | 1 | -1 | 3 | -3 | 9 | -9 |
| y+2 | -9 | 9 | -3 | 3 | -1 | 1 |
| x | 0 | -2 | 2 | -4 | 8 | -10 |
| y | -11 | 7 | -5 | 1 | -3 | -1 |
17 tháng 5 2016
a) $xy+3x-2y-11=0$$x\left(y+3\right)-2y-6-5=0$$x\left(y+3\right)-2\left(y+3\right)=5$$\left(x-2\right)\left(y+3\right)=5$$x-2;y+3\in U\left(5\right)$
b) $xy+2x+y+11=0$
$x\left(y+2\right)+y+2+9=0$$x\left(y+2\right)+\left(y+2\right)=-9$$\left(x+1\right)\left(y+2\right)=-9$$x+1;y+2\in U\left(-9\right)$
| x-2 | 1 | -1 | 5 | -5 | ||
| y+3 | 5 | -5 | 1 | -1 | ||
| x | 3 | 1 | 7 | -3 | ||
| y | 2 | -8 | -2 | -4 | ||
| x+1 | 1 | -1 | 3 | -3 | 9 | -9 |
| y+2 | -9 | 9 | -3 | 3 | -1 | 1 |
| x | 0 | -2 | 2 | -4 | 8 | -10 |
| y | -11 | 7 | -5 | 1 |
15 tháng 1 2016
1. xy + 5x + 5y = 92
=> (xy + 5x) + (5y + 25) = 92 + 25
=> x(y + 5) + 5(y + 5) = 117
=> (x + 5)(y + 5) = 117
=> x + 5 \(\in\)Ư(117) = {-1;1;-3;3;-9;9;-13;13;-39;39;-117;117}
Mà x >= 0 => x + 5 >= 5
=> x + 5 \(\in\){9;13;39;117}
Ta có bảng sau:
| x + 5 | 9 | 13 | 39 | 117 |
| x | 4 | 8 | 34 | 112 |
| y + 5 | 13 | 9 | 3 | 1 |
| y | 8 | 4 | -2 (loại) | -4 (loại) |
Vậy; (x;y) \(\in\){(4;8);(8;4)}
PT
1
M
0
KN
10 tháng 3 2019
Giải
Theo đề bài, ta có: \(xy-3x+2y-11=0\)
\(\Leftrightarrow x\left(y-3\right)+2y-6=5\)
\(\Leftrightarrow x\left(y-3\right)+2\left(y-3\right)=5\)
\(\Leftrightarrow\left(x+2\right)\left(y-3\right)=5\)
\(\Leftrightarrow\hept{\begin{cases}x+2\\y-3\end{cases}}\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)
Lập bảng:
| \(x+2\) | \(1\) | \(-1\) | \(5\) | \(-5\) |
| \(y-3\) | \(5\) | \(-5\) | \(1\) | \(-1\) |
| \(x\) | \(-1\) | \(-3\) | \(3\) | \(-7\) |
| \(y\) | \(8\) | \(-2\) | \(4\) | \(2\) |
Vậy \(\left(x,y\right)\in\left\{\left(-1,8\right);\left(-3,-2\right);\left(3,4\right);\left(-7,2\right)\right\}\)
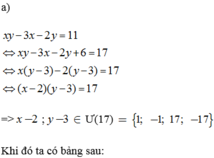
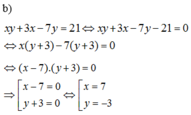
<=> xy + 3x - 2y = 0 + 11
<=> xy + 3x - 2y = 11
<=> x(y+3)-2(y+3)=5
<=>(x-2)(y+3)=5
suy ra (x-2) và (y+3) là các ước nguyên của 5.
Th1. x-2=1 <=>x=3
.......y+3=5 <=> y=2
Th2 x-2=-1 <=> x=1
.......y+3=-5 <=> y= -8
Th3. x-2=5 <=> x=7
.......y+3=1 <=> y= -2
Th4. x-2= -5 <=> x= -3
.......y+3= -1 <=> y= -4
Vậy (x,y) = (3, 2); (1, -8); (7, -2); (-3, -4)
Thanks