
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\left\{{}\begin{matrix}x_1+x_2=-b\\x_1x_2=c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=10\\c=-24\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}x_1+x_2=-b\\x_1x_2=c\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-b=-5\\c=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=5\\c=0\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=1-2=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2\\c=-1\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}x_1+x_2=3-\dfrac{1}{2}=\dfrac{5}{2}\\x_1x_2=-\dfrac{3}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-\dfrac{5}{2}\\c=-\dfrac{3}{2}\end{matrix}\right.\)

ĐK: \(x\ge0\)
\(M=\frac{\sqrt{x}-1}{\sqrt{x}+2}=\frac{\sqrt{x}+2-3}{\sqrt{x}+2}=1-\frac{3}{\sqrt{x}+2}\)
Để M min \(\Leftrightarrow\frac{3}{\sqrt{x}+2}\)max
\(\Leftrightarrow\sqrt{x}+2\)min
\(\Leftrightarrow\sqrt{x}\)min
\(\Leftrightarrow x\)min
mà \(x\ge0\)
\(\Leftrightarrow x=0\)
Vậy \(Min_M=\frac{-1}{2}\Leftrightarrow x=0\)

Cả 4 đa thức đều có bậc bằng 3 bạn nhé. Điều đấy rõ quá còn gì.

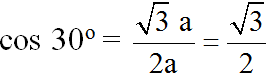


\(\sin\widehat{B}=\dfrac{AC}{BC}\Rightarrow BC=\dfrac{AC}{\sin\widehat{B}}=\dfrac{4}{\sin42^o}\)
\(AC^2=CH.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow CH=\dfrac{AC^2}{BC}=4.\sin42^o\)
Xét tg vuông AHC có
\(x=AH=\sqrt{AC^2-CH^2}\) (Pitago)
\(\Rightarrow x=\sqrt{16-16\sin^242^o}=4\sqrt{1-\sin^242}=4\sqrt{\cos^242^o}=4\cos42^o\)