VK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BG
0
19 tháng 3 2019
\(\Leftrightarrow C=\frac{\left(x-1\right)\left(x+3\right)}{\left(x+1\right)\left(x-1\right)}=\frac{x+3}{x+1}=\frac{\left(x+1\right)+2}{\left(x+1\right)}\)
Để \(C\in Z\Leftrightarrow2⋮ \left(x+1\right)\Leftrightarrow\left(x+1\right)\inƯ\left(2\right)\)
\(\Leftrightarrow\left(x+1\right)\in\left(\pm1;\pm2\right)\)
\(\Leftrightarrow x\in\left(-2;0;1;-3\right)\)
KV
27 tháng 10 2023
a) 2ˣ + 2ˣ⁺³ = 72
2ˣ.(1 + 2³) = 72
2ˣ.9 = 72
2ˣ = 72 : 9
2ˣ = 8
2ˣ = 2³
x = 3
b) Để số đã cho là số nguyên thì (x - 2) ⋮ (x + 1)
Ta có:
x - 2 = x + 1 - 3
Để (x - 2) ⋮ (x + 1) thì 3 ⋮ (x + 1)
⇒ x + 1 ∈ Ư(3) = {-3; -1; 1; 3}
⇒ x ∈ {-4; -2; 0; 2}
Vậy x ∈ {-4; -2; 0; 2} thì số đã cho là số nguyên
c) P = |2x + 7| + 2/5
Ta có:
|2x + 7| ≥ 0 với mọi x ∈ R
|2x + 7| + 2/5 ≥ 2/5 với mọi x ∈ R
Vậy GTNN của P là 2/5 khi x = -7/2
1 tháng 2 2017
a. để A dương thì \(2x-1\ge0\Rightarrow2x\ge1\Rightarrow x\ge\frac{1}{2}\)
b. Để B âm thì \(9-2c< 0\Rightarrow9< 2c\Rightarrow c>\frac{9}{2}\)
15 tháng 3 2017
\(C=\frac{2\left(x-1\right)^2+1}{x^2-2x+3}=\frac{2\left(x-1\right)^2+1}{\left(x^2-2x+1\right)+2}=\frac{2\left(x-1\right)^2+4-3}{\left(x-1\right)^2+2}=\frac{2\left[\left(x-1\right)^2+2\right]-3}{\left(x-1\right)^2+2}=2-\frac{3}{\left(x-1\right)^2+2}\)
Để \(2-\frac{3}{\left(x-1\right)^2+2}\) đạt GTNN <=> \(\left(x-1\right)^2+2\)đạt GTNN
\(\left(x-1\right)^2\ge0\Rightarrow\left(x-1\right)^2+2\ge2\) có GTNN là 2 tại x = 1
\(\Rightarrow B_{min}=2-\frac{3}{\left(1-1\right)^2+2}=\frac{1}{2}\) tại \(x=1\)
3 tháng 10 2021
Bài 1:
a: \(x^2+5x=x\left(x+5\right)\)
Để biểu thức này âm thì \(x\left(x+5\right)< 0\)
hay -5<x<0
b: \(3\left(2x+3\right)\left(3x-5\right)< 0\)
\(\Leftrightarrow-\dfrac{3}{2}< x< \dfrac{5}{3}\)
K
2
20 tháng 12 2021
\(\Leftrightarrow x+1\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{0;-2;2;-4\right\}\)
20 tháng 12 2021
⇔x+1∈{1;−1; 3 ;−3}⇔x+1∈{1 ;− 1 ; 3 ;−3}
hay x∈{0;−2; 2;−4}
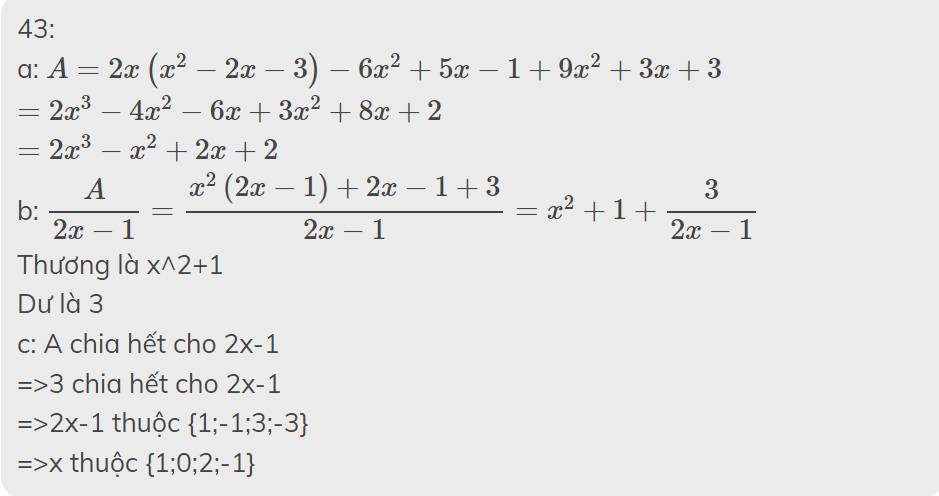
\(A=\frac{x+2}{2x-1}\)đk: x khác 1/2.
Vậy A < 0 khi \(-2< x< \frac{1}{2}\)