
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

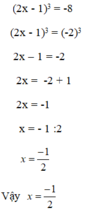


vi 2x-1 lẻ nen |x-1|hoac |x-3| lẻ
+)Neu |x-1|lẻ thì |x-3| lẻ(loai vi ca hai cung le)
+)neu |x-3| lẻ thì|x-1|lẻ(loai vi ca hai cung le)
vay ko co so nao tm x−1|+|x−3|=2x−1

a) x3 = -27
<=> -33 = -27
=> x = -3
b) (2x - 1)3 = 8
<=> 8x3 - 12x2 + 6x - 1 = 8
<=> 8x3 - 12x2 + 6x - 1 - 8 = 0
<=> (2x - 3)(4x2 + 3) = 0
<=> 2x - 3 = 0 hoặc 4x2 + 3 = 0
2x = 0 + 3
2x = 3
x = 3/2
=> x = 3/2
c) x3 = x5
<=> x3 - x5 = 0
<=> x3(1 - x2) = 0
<=> x = 0; 1; -1
=> x = 0; 1; -1
d) (x - 2)2 = 16
<=> (x - 2)2 = 42
<=> x - 2 = 4 hoặc x - 2 = -4
x = 4 + 2 x = -4 + 2
x = 6 x = -2
=> x = 6; -2
g) (2x - 3)2 = 9
<=> (2x - 3)2 = 32
<=> 2x - 3 = 3 hoặc 2x - 3 = -3
2x = 3 + 3 2x = -3 + 3
2x = 6 2x = 0
x = 3 x = 0
=> x = 3; 0
y) 3x3 - 4x = 0
<=> x(3x - 4) = 0
<=> x = 0 hoặc 3x - 4 = 0
3x = 0 + 4
3x = 4
x = 4/3

a. (x-1/20)2=0
=> x-1/20=0
=> x=1/20
b. (x-2)2=1
=> (x-2)2=12=(-1)2
+) x-2=1
=> x=3
+) x-2=-1
=> x=1
Vậy x \(\in\){1;3}
c. (2x-1)3=-8
=> (2x-1)3=(-2)3
=> 2x-1=-2
=> 2x=-1
=> x=-1/2
d. (x+1/2)2=1/16
=> (x+1/2)2=(1/4)2=(-1/4)2
+) x+1/2=1/4
=> x=-1/4
+) x+1/2=-1/4
=> x=-3/4
Vậy x \(\in\){-3/4; -1/4}

1) Các cách viết số 25 dưới dãng lũy thừa là: 251; 52; (-5)2
2) a) \(\left(x-\frac{1}{2}\right)^2=0\)
=> \(x-\frac{1}{2}=0\)
=> \(x=\frac{1}{2}\)
Vậy \(x=\frac{1}{2}\)
b) (x - 2)2 = 1
=> \(\left[\begin{array}{nghiempt}x-2=1\\x-2=-1\end{array}\right.\)=> \(\left[\begin{array}{nghiempt}x=3\\x=1\end{array}\right.\)
Vậy \(x\in\left\{3;1\right\}\)
c) (2x - 1)3 = -8
=> (2x - 1)3 = (-2)3
=> 2x - 1 = -2
=> 2x = -2 + 1
=> 2x = -1
=> \(x=-\frac{1}{2}\)
Vậy \(x=-\frac{1}{2}\)
d) \(\left(x+\frac{1}{2}\right)^2=16\)
=> \(\left[\begin{array}{nghiempt}x+\frac{1}{2}=\frac{1}{4}\\x+\frac{1}{2}=-\frac{1}{4}\end{array}\right.\)=> \(\left[\begin{array}{nghiempt}x=-\frac{1}{4}\\x=-\frac{3}{4}\end{array}\right.\)
Vậy \(x\in\left\{-\frac{1}{4};-\frac{3}{4}\right\}\)
1) Các cách viết số 25 dưới dãng lũy thừa là: 251; 52; (-5)2
2) a) (x−12)2=0(x−12)2=0
=> x−12=0x−12=0
=> x=12x=12
Vậy x=12x=12
b) (x - 2)2 = 1
=> [x−2=1x−2=−1[x−2=1x−2=−1=> [x=3x=1[x=3x=1
Vậy x∈{3;1}x∈{3;1}
c) (2x - 1)3 = -8
=> (2x - 1)3 = (-2)3
=> 2x - 1 = -2
=> 2x = -2 + 1
=> 2x = -1
=> x=−12x=−12
Vậy x=−12x=−12
d) (x+12)2=16(x+12)2=16
=> [x+12=14x+12=−14[x+12=14x+12=−14=> [x=−14x=−34[x=−14x=−34
Vậy x∈{−14;−34}

\(\dfrac{1-x}{3}=\dfrac{2y-1}{8}\)
=>8(1-x)=3(2y-1)
=>8-8x=6y-3
=>-8x-6y=-11
=>8x+6y=11
mà 2x+y=6
nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}8x+6y=11\\2x+y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x+6y=11\\8x+4y=24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2y=-13\\2x+y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{13}{2}\\2x=6-y=6+\dfrac{13}{2}=\dfrac{25}{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{25}{4}\\y=-\dfrac{13}{2}\end{matrix}\right.\)