
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


D= 4/|x -2| + 2 lớn nhất khi 4/|x -2| lớn nhất suy ra |x -2| là số nguyên dương nhỏ nhất => |x -2|=1=>x-2=1 hoặc x-2=-1 => x=3 hoặc x=1
Vậy với x=3 hoặc x=1 thì D có giá trị lớn nhất là D=4/|3 -2| + 2=4+2=6 hoặc D=4/|1 -2| + 2=4+2=6

a)Ta thấy: \(\left|x-5\right|\ge0\Rightarrow A\ge0\)
Dấu "=" xảy ra khi \(x=5\)
Vậy \(Min_A=0\) khi \(x=5\)
b)Ta thấy: \(\left|5+x\right|\ge0\Rightarrow B\ge0\)
Dấu "=" xảy ra khi \(x=-5\)
Vậy \(Min_B=0\) khi \(x=-5\)
c)Ta thấy: \(\left|-x+2\right|\ge0\Rightarrow C\ge0\)
Dấu "=" xảy ra khi \(x=2\)
Vậy \(Min_C=0\) khi \(x=2\)
d)Ta thấy: \(\left|x+1\right|\ge0\Rightarrow D\ge0\)
Dấu "=" xảy ra khi \(x=-1\)
Vậy \(Min_D=0\) khi \(x=-1\)

tất cả đều có giá trị lớn nhất bằng 0
a.) tại x=-1
b.) tại x=-5
c.) tại x=-2
d.) tại x=3
a ) Vì |x + 1| ≥ 0 với mọi x
=> - |x + 1| ≤ 0 với mọi x
Dấu "=" xảy ra khi và chỉ khi |x + 1| = 0 => x = - 1
Vậy giá trị lớn nhất của A là 0 tại x = - 1
Các ý khác tương tự

Bài 1:
a, Ta có: (x - 1)2 \(\ge\)0 với mọi x
=> A = (x - 1)2 + 2016 \(\ge\)2016
Dấu "=" xảy ra <=> (x-1)2 = 0 <=> x = 1
Vậy GTNN của A = 2016 tại x = 1
b, Ta có: |x + 4| \(\ge\)0 với mọi x
=> B = |x + 4| + 2017 \(\ge\)2017
Dấu "=" xảy ra <=> |x + 4| = 0 <=> x = -4
Vây GTNN của B = 2017 tại x = -4
Bài 2:
a, Ta có: (x + 1)2016 \(\ge\)0 với mọi x
=> P = 2010 - (x + 1)2016 \(\ge\)2010
Dấu "=" xảy ra <=> (x + 1)2016 = 0 <=> x = -1
Vậy GTLN của P = 2010 tại x = -1
b, Ta có: |3 - x| \(\ge\)0 với mọi x
=> Q = 2010 - |3 - x| \(\ge\)2010
Dấu "=" xảy ra <=> |3 - x| = 0 <=> x = 3
Vậy GTLN của Q = 2010 tại x = 3
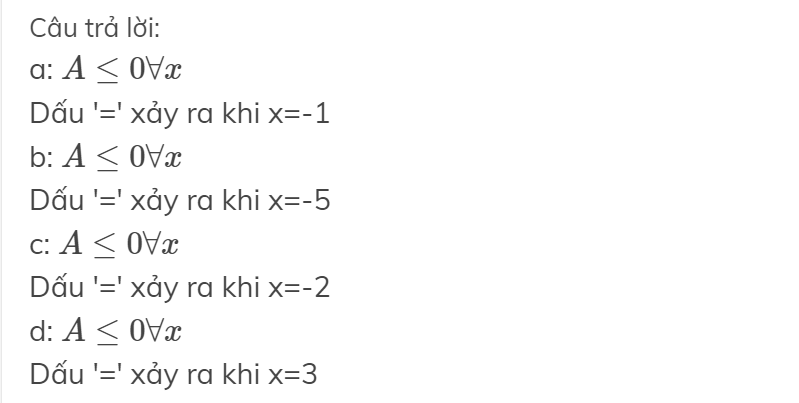
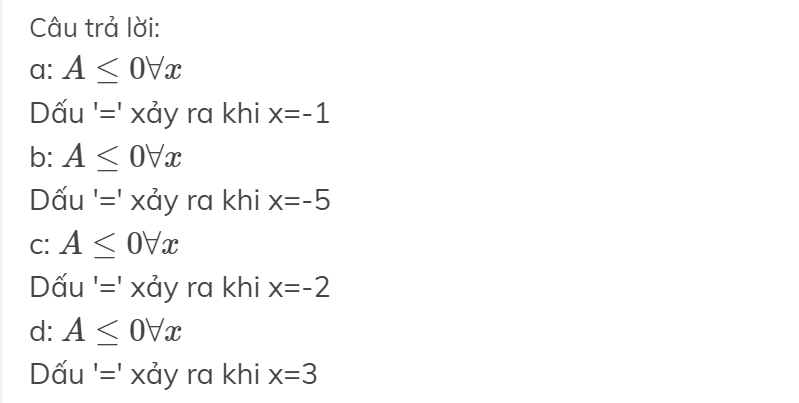
Do \(\left|x-2\right|\ge0\Rightarrow\left|x-2\right|+2\ge2\Rightarrow D\le\frac{4}{2}=2\)
Đẳng thức xảy ra tại x=2
Vậy \(D_{max}=2\) tại x=2
Ix+2I +2 la so duong vi :+2>0
+gttd luon la so duong
-.4 / Ix-2I+2 >0
ma 4 / Ix-2I+2 dat gtln->4 chia het cho Ix-2I+2
Ix-2I+2 E U(4)= 1,2,4
loai 4 vi 4/4=1
loai 1 vi neu Ix-2I+2=1->Ix-2I=1-2=-1->x E thr
=>Ix-2I+2=2
Ix-2I=2-2=0
=>x-2=0 ===> x=0+2=2
KL: de D co gtln, x phai =2