Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì số dư là số dư lớn nhất có thể nên số dư nhỏ hơn số chia 1 đơn vị. Vậy nếu thêm 1 đơn vị vào số bị chia thì sẽ chia hết và thương tăng thêm 1 đơn vị, tức là thương bằng 19 và số bị chia lúc đó là 2374 + 1 = 2375.
Số chia là:
2375 : 19 = 125
Thử lại: 2374 : 125 = 18 dư 124
Vì số dư là số dư lớn nhất có thể nên số dư nhỏ hơn số chia 1 đơn vị. Vậy nếu thêm 1 đơn vị vào số bị chia thì sẽ chia hết và thương tăng thêm 1 đơn vị, tức là thương bằng 19 và số bị chia lúc đó là 2374 + 1 = 2375.
Số chia là:
2375 : 19 = 125
Thử lại: 2374 : 125 = 18 dư 124

4a.
Số tự nhiên là A, ta có:
A = 7m + 5
A = 13n + 4
=>
A + 9 = 7m + 14 = 7(m + 2)
A + 9 = 13n + 13 = 13(n+1)
vậy A + 9 là bội số chung của 7 và 13
=> A + 9 = k.7.13 = 91k
<=> A = 91k - 9 = 91(k-1) + 82
vậy A chia cho 91 dư 82
4b.
Giả sử p là 1 số nguyên tố >3, do p không chia hết cho 3 nên p có dạng 3k + 1 hoặc 3k + 2
Vì p +4 là số nguyên tố nên p không thể có dạng 3k + 2
Vậy p có dạng 3k +1.
=> p + 8 = 3k + 9 chia hết cho 3 nên nó là hợp số.

Đặt $f(x)=x^3+ax+b$. Theo định lý Bezout về dư trong đa thức thì số dư của $f(x)$ cho $x-a$ chính là $f(a)$. Do đó:
\(\left\{\begin{matrix} f(-1)=-1-a+b=7\\ f(3)=27+3a+b=5\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=\frac{-15}{2}\\ b=\frac{1}{2}\end{matrix}\right.\)
Vì \(a,b\not\in \mathbb{Z}\Rightarrow \) bài toán đúng với TH $x$ chẵn.
Đặt f(x)=x3+ax+bf(x)=x3+ax+b. Theo định lý Bezout về dư trong đa thức thì số dư của f(x)f(x) cho x−ax−achính là f(a)f(a). Do đó:
{f(−1)=−1−a+b=7f(3)=27+3a+b=5⇒{a=−152b=12{f(−1)=−1−a+b=7f(3)=27+3a+b=5⇒{a=−152b=12
tick đúng

Giải:
Số chia là 9 (Vì số chia là số có 1 chữ số mà số dư là 8)
Thương là:
9 x 4 = 36
Số bị chia là:
36 x 9 + 8 = 332
ĐS: 332

Gọi số bị chia là a ( a ∈ N | a : 6 dư 4 )
Vì khi chia a cho 6 , số dư là 4 nên a + 2 chia hết cho 6
Vậy ta thêm 2 đơn vị vào số bị chia để được phép chia hết .
Số chia 6 dư 4 có dạng là:6k+4(k\(\in\)N)
Vậy số bị chia có dạng là:6k+4
Ta có:6k+4+2=6k+6=6(k+1) chia hết cho 6
Vậy phải thêm vào số bị chia 2 đơn vị để được một phép chia hết

Lời giải:
Tích của số chia và thương: $267-8=259$
Số chia là: $37$
Thương: $7$

Do f x chi cho x - 2 được phần dư là 2019 nên ta viết lại:
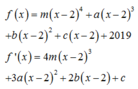
Do f ' x chi cho x - 2 dư 2018 nên c = 2018 .
Suy ra
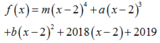
Từ đó phần dư khi chia
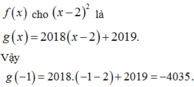
Chọn B.

Gọi x là số cần tìm (x ∈ ℕ*)
x + 1 = BCNN(2; 3; 4; 5; 6)
Ta có:
2 = 2
3 = 3
4 = 2²
5 = 5
6 = 2.3
⇒ x + 1 = BCNN(2; 3; 4; 5; 6) = 2².3.5 = 60
⇒ x = 60 - 1
⇒ x = 59
Vậy số cần tìm là 59
x=17
Ta có :
235 : x dư 14
=> x > 14
Và (235 - 14) \(⋮\) x => 221 \(⋮\) x
Mà Ư(221) \(\in\) \(\left\{13;17\right\}\)
=> x \(\in\) \(\left\{13;17\right\}\)
Mà x > 14 => x = 17 Vậy số cần tìm là 17