K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
27 tháng 5 2018
Ta có \(A=\frac{\sqrt{x}-1}{\sqrt{x}+1}=\frac{\sqrt{x}+1-2}{\sqrt{x}+1}=1-\frac{2}{\sqrt{x}+1}\)
Để A nguyên thì \(\frac{2}{\sqrt{x}+1}\)phải nguyên suy ra \(\sqrt{x}+1\)là ước của 2
Ta thấy \(Ư\left(2\right)=\left\{1;-1;2;-2\right\}\) mà điều kiện cho \(x\ge0\)và \(x\ne1\)nên \(\sqrt{x}+1\in\left\{1;2\right\}\)
Với \(\sqrt{x}+1=1\Rightarrow\sqrt{x}=0\Rightarrow x=0\)(thoải mãn )
Với \(\sqrt{x}+1=2\Rightarrow\sqrt{x}=1\Rightarrow x=1\)(loại)
Vậy x = 0 thì A nguyên
30 tháng 8 2021
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne9\end{matrix}\right.\)
Ta có: \(A=\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+9}{x-9}\)
\(=\dfrac{x-3\sqrt{x}+2x+6\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{3}{\sqrt{x}+3}\)
b: Thay x=16 vào A, ta được:
\(A=\dfrac{3}{4+3}=\dfrac{3}{7}\)
3 tháng 2 2021
a) ĐKXĐ: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
Ta có: \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{1}{x-\sqrt{x}}\right)\cdot\left(\dfrac{1}{1+\sqrt{x}}+\dfrac{2}{x-1}\right)\)
\(=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\cdot\left(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
b) Để P>0 thì \(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}>0\)
mà \(\sqrt{x}+1>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}\left(\sqrt{x}-1\right)>0\)
mà \(\sqrt{x}>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}-1>0\)
\(\Leftrightarrow\sqrt{x}>1\)
hay x>1
Kết hợp ĐKXĐ,ta được: x>1
Vậy: Để P>0 thì x>1
TM
1
12 tháng 8 2023
a:
ĐKXĐ: x>0; x<>1\(M=\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{3\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\left(\sqrt{x}+1\right)^2-4\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{x+2\sqrt{x}+1-4\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}-3\sqrt{x}+1}{\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}}{x-2\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
b: M là số nguyên
=>\(\sqrt{x}-1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)
=>căn x-2 thuộc {1;-1}
=>căn x thuộc {3;1}
=>x thuộc {9;1}
Kết hợp ĐKXĐ, ta được: x=9
c: M<0
=>\(\dfrac{\sqrt{x}-1}{\sqrt{x}-2}< 0\)
=>\(1< \sqrt{x}< 2\)
=>1<x<4
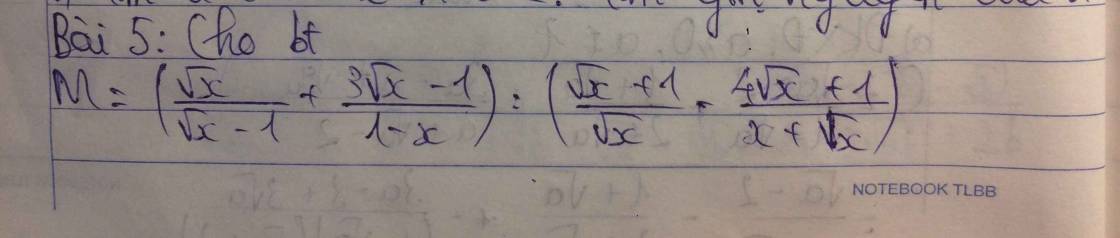
\(\dfrac{-3}{\sqrt{x}+3}< \dfrac{1}{2}\)
\(\Leftrightarrow-6< \sqrt{x}+3\Leftrightarrow\sqrt{x}>-9\left(đúng\forall x\right)\)
Vậy \(x\in Z^+,x\ne9\)
Uhm cảm ơn bạn nhưng mình không hiểu tại sao máy lại ra thế này:<
Nếu mình nhớ không nhầm thì chúng ta không nhân chéo được đúng khôm ạ:33? Hay thêm trường hợp x khác 0 ạ @_@?