Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a: \(\Leftrightarrow\left|x+\dfrac{4}{15}\right|=-2.15+3.75=\dfrac{8}{5}\)
=>x+4/15=8/5 hoặc x+4/15=-8/5
=>x=4/3 hoặc x=-28/15
b: \(\Leftrightarrow\left[{}\begin{matrix}\dfrac{5}{3}x=-\dfrac{1}{6}\\\dfrac{5}{3}x=\dfrac{1}{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{6}:\dfrac{5}{3}=\dfrac{-3}{30}=\dfrac{-1}{10}\\x=\dfrac{1}{10}\end{matrix}\right.\)
c: \(\Leftrightarrow\left|x-1\right|-1=1\)
=>|x-1|=2
=>x-1=2 hoặc x-1=-2
=>x=3 hoặc x=-1
Bài 2:
b: \(\Leftrightarrow\left\{{}\begin{matrix}x-y=0\\y+\dfrac{9}{25}=0\end{matrix}\right.\Leftrightarrow x=y=-\dfrac{9}{25}\)
Bài 3:
a: \(A=\left|x+\dfrac{15}{19}\right|-1>=-1\)
Dấu '=' xảy ra khi x=-15/19
b: \(\left|x-\dfrac{4}{7}\right|+\dfrac{1}{2}>=\dfrac{1}{2}\)
Dấu '=' xảy ra khi x=4/7

\(a.-8:\left(4\dfrac{1}{5}x+\dfrac{3}{10}\right)=4\dfrac{4}{9}\)
\(4\dfrac{1}{5}x+\dfrac{3}{10}=\left(-8\right):4\dfrac{4}{9}\)
\(4\dfrac{1}{5}x+\dfrac{3}{10}=\dfrac{-9}{5}\)
\(4\dfrac{1}{5}x=\dfrac{-9}{5}-\dfrac{3}{10}\)
\(4\dfrac{1}{5}x=\dfrac{-21}{10}\)
\(x=\dfrac{-21}{10}:\dfrac{21}{5}\)
\(x=\dfrac{-1}{2}\)
Vay \(x=\dfrac{-1}{2}\).
\(b.4\dfrac{2}{3}-\left(\dfrac{3}{5}:x\right)=-20\%\)
\(\dfrac{14}{3}-\left(\dfrac{3}{5}:x\right)=\dfrac{-1}{5}\)
\(\dfrac{3}{5}:x=\dfrac{14}{3}-\dfrac{-1}{5}\)
\(\dfrac{3}{5}:x=\dfrac{73}{15}\)
\(x=\dfrac{3}{5}:\dfrac{73}{15}\)
\(x=\dfrac{9}{73}\)
Vay \(x=\dfrac{9}{73}\).
Câu c; d; e tương tự nhé.

a)Ta thấy:
\(\dfrac{1}{x}-\dfrac{1}{x+a}=\dfrac{x+a}{x\left(x+a\right)}-\dfrac{x}{x\left(x+a\right)}\)
\(=\dfrac{\left(x+a\right)-x}{x\left(x+a\right)}\)
\(=\dfrac{a}{x\left(x+a\right)}\)
\(\Rightarrowđpcm\)
b)Ta thấy:
\(\dfrac{1}{x\left(x+1\right)}-\dfrac{1}{\left(x+1\right)\left(x+2\right)}\)
\(=\dfrac{\left(x+1\right)\left(x+2\right)}{x\left(x+1\right)^2\left(x+2\right)}-\dfrac{x\left(x+1\right)}{x\left(x+1\right)^2\left(x+2\right)}\)
\(=\dfrac{x+2}{x\left(x+1\right)\left(x+2\right)}-\dfrac{x}{x\left(x+1\right)\left(x+2\right)}\)
\(=\dfrac{\left(x+2\right)-x}{x\left(x+1\right)\left(x+2\right)}=\dfrac{2}{x\left(x+1\right)\left(x+2\right)}\Rightarrowđpcm\)
c)Ta thấy:
\(\dfrac{1}{x\left(x+1\right)\left(x+2\right)}-\dfrac{1}{\left(x+1\right)\left(x+2\right)\left(x+3\right)}\)
\(=\dfrac{\left(x+1\right)\left(x+2\right)\left(x+3\right)}{x\left(x+1\right)^2\left(x+2\right)^2\left(x+3\right)}-\dfrac{x\left(x+1\right)\left(x+2\right)}{x\left(x+1\right)^2\left(x+2\right)^2\left(x+3\right)}=\dfrac{x+3}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}-\dfrac{x}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}=\dfrac{x+3-x}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}=\dfrac{3}{x\left(x+1\right)\left(x+2\right)\left(x+3\right)}\Rightarrowđpcm\)
a/ \(\dfrac{1}{x}-\dfrac{1}{x+a}=\dfrac{a}{x\left(x+a\right)}\)
Ta có: \(\dfrac{1}{x}-\dfrac{1}{x+a}=\dfrac{x+a}{x\left(x+a\right)}-\dfrac{x}{x\left(x+a\right)}\)
\(=\dfrac{\left(x-x\right)+a}{x\left(x+a\right)}\) hay \(\dfrac{a}{x\left(x+a\right)}\)
\(\Rightarrow\dfrac{1}{x}-\dfrac{1}{x+a}=\dfrac{a}{x\left(x+a\right)}\left(đpcm\right)\)

\(B=\left(1+\dfrac{1}{8}\right)\left(1+\dfrac{1}{15}\right)\left(1+\dfrac{1}{24}\right).....\left(1+\dfrac{1}{440}\right)\left(1+\dfrac{1}{483}\right)\)
\(B=\dfrac{9}{8}.\dfrac{16}{15}.\dfrac{25}{24}.....\dfrac{441}{440}.\dfrac{484}{483}\)
\(B=\dfrac{9.16.25.....441.484}{8.15.24.....440.483}\)
\(B=\dfrac{3.3.4.4.5.5.....21.21.22.22}{2.4.3.5.4.6.....20.22.21.23}\)
\(B=\dfrac{3.4.5.....21.22}{2.3.4.....20.21}.\dfrac{3.4.5.....21.22}{4.5.6.....22.23}\)
\(B=11.\dfrac{3}{23}=\dfrac{33}{23}\)
B = \(\dfrac{4}{3}.\dfrac{9}{8}.\dfrac{16}{15}.\dfrac{25}{24}...\dfrac{121}{120}.\dfrac{144}{143}\)
B = \(\dfrac{4.9.16.25...121.144}{3.8.15.24....120.143}\)
B = \(\dfrac{2.2.3.3.4.4.5.5...11.11.12.12}{1.3.2.4.3.5.4.6...10.12.11.13}\)
B = \(\dfrac{2.3.4.5...11.12}{1.2.3.4.5...10.11}.\dfrac{2.3.4.5...11.12}{3.4.5.6.7...12.13}\)
B = 12 . \(\dfrac{2}{13}\)
B = \(\dfrac{24}{13}\)

(1 - \(\dfrac{1}{2}\)) . (1 - \(\dfrac{1}{3}\)) . (1 - \(\dfrac{1}{4}\)) ... (1 - \(\dfrac{1}{x}\)) = \(\dfrac{1}{2014}\)
=> \(\dfrac{1}{2}\) . \(\dfrac{2}{3}\) . \(\dfrac{3}{4}\) ... \(\dfrac{x-1}{x}\) =\(\dfrac{1}{2014}\)
=> \(\dfrac{1.2.3...x-1}{2.3.4...x}\) = \(\dfrac{1}{2014}\)
=:> \(\dfrac{1}{x}\) = \(\dfrac{1}{2014}\)
Vậy x = 2014
(Mình nghĩa là vậy, có gì sai mong bạn bỏ qua nha)

Mấy bài này bạn tự làm đi, chuyển vế tìm x gần giống cấp I mà.
b)\(\dfrac{-3}{5}.x=\dfrac{1}{4}+0,75\)
=>\(\dfrac{-3}{5}.x=1\)
=>\(x=1:\dfrac{-3}{5}\)
=>\(x=\dfrac{-5}{3}\)
Vậy \(x=\dfrac{-5}{3}\)

a: (x+1/2)(2/3-2x)=0
=>x+1/2=0 hoặc 2/3-2x=0
=>x=-1/2 hoặc x=1/3
b: 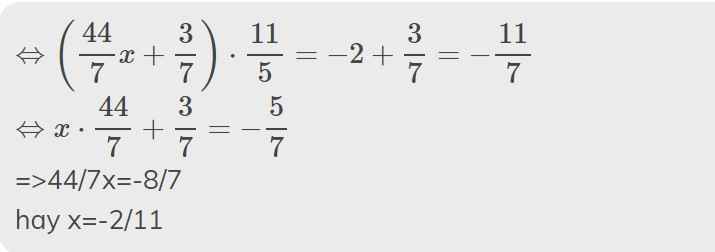
c: \(\Leftrightarrow x\cdot\left(\dfrac{13}{4}-\dfrac{7}{6}\right)=\dfrac{5}{12}+\dfrac{5}{3}=\dfrac{5}{12}+\dfrac{20}{12}=\dfrac{25}{12}\)
\(\Leftrightarrow x=\dfrac{25}{12}:\dfrac{39-14}{12}=\dfrac{25}{25}=1\)

a) \(\left(2x-3\right)\left(6-2x\right)=0\)
\(\circledast\)TH1: \(2x-3=0\\ 2x=0+3\\ 2x=3\\ x=\dfrac{3}{2}\)
\(\circledast\)TH2: \(6-2x=0\\ 2x=6-0\\ 2x=6\\ x=\dfrac{6}{2}=3\)
Vậy \(x\in\left\{\dfrac{3}{2};3\right\}\).
b) \(\dfrac{1}{3}x+\dfrac{2}{5}\left(x-1\right)=0\)
\(\dfrac{1}{3}x=0-\dfrac{2}{5}\left(x-1\right)\)
\(\dfrac{1}{3}x=-\dfrac{2}{5}\left(x-1\right)\)
\(-\dfrac{2}{5}-\dfrac{1}{3}=-x\left(x-1\right)\)
\(-\dfrac{11}{15}=-x\left(x-1\right)\)
\(\Rightarrow x=1.491631652\)
Vậy \(x=1.491631652\)
c) \(\left(3x-1\right)\left(-\dfrac{1}{2}x+5\right)=0\)
\(\circledast\)TH1: \(3x-1=0\\ 3x=0+1\\ 3x=1\\ x=\dfrac{1}{3}\)
\(\circledast\)TH2: \(-\dfrac{1}{2}x+5=0\\ -\dfrac{1}{2}x=0-5\\ -\dfrac{1}{2}x=-5\\ x=-5:-\dfrac{1}{2}\\ x=10\)
Vậy \(x\in\left\{\dfrac{1}{3};10\right\}\).
d) \(\dfrac{x}{5}=\dfrac{2}{3}\\ x=\dfrac{5\cdot2}{3}\\ x=\dfrac{10}{3}\)
Vậy \(x=\dfrac{10}{3}\).
e) \(\dfrac{x}{3}-\dfrac{1}{2}=\dfrac{1}{5}\\ \)
\(\dfrac{x}{3}=\dfrac{1}{5}+\dfrac{1}{2}\)
\(\dfrac{x}{3}=\dfrac{7}{10}\)
\(x=\dfrac{3\cdot7}{10}\)
\(x=\dfrac{21}{10}\)
Vậy \(x=\dfrac{21}{10}\).
f) \(\dfrac{x}{5}-\dfrac{1}{2}=\dfrac{6}{10}\)
\(\dfrac{x}{5}=\dfrac{6}{10}+\dfrac{1}{2}\)
\(\dfrac{x}{5}=\dfrac{11}{10}\)
\(x=\dfrac{5\cdot11}{10}\)
\(x=\dfrac{55}{10}=\dfrac{11}{2}\)
Vậy \(x=\dfrac{11}{2}\).
g) \(\dfrac{x+3}{15}=\dfrac{1}{3}\\ x+3=\dfrac{15}{3}=5\\ x=5-3\\ x=2\)
Vậy \(x=2\).
h) \(\dfrac{x-12}{4}=\dfrac{1}{2}\\ x-12=\dfrac{4}{2}=2\\ x=2+12\\ x=14\)
Vậy \(x=14\).

Bài 1:
\(\left(-\dfrac{72}{40}-\dfrac{144}{60}-2\dfrac{1}{3}\right):\left(\dfrac{45}{100}-\dfrac{25}{60}+-\dfrac{75}{25}\right)\)
\(=\left(-\dfrac{9}{5}-\dfrac{12}{5}-\dfrac{7}{3}\right):\left(\dfrac{9}{20}-\dfrac{5}{12}+-3\right)\)
\(=\left(-\dfrac{27}{15}-\dfrac{36}{15}-\dfrac{21}{15}\right):\left(\dfrac{27}{60}-\dfrac{25}{60}+-3\right)\)
\(=\left(-\dfrac{28}{5}\right):\left(-\dfrac{89}{30}\right)\)
\(=\left(-\dfrac{28}{5}\right).\left(-\dfrac{30}{89}\right)\)
\(=\dfrac{168}{89}\)

1. a, 3x + |x - 2| = 8
<=> |x - 2| = 8 - 3x
Xét 2 TH :
TH1: x - 2 = 8 - 3x
<=> x + 3x = 8 + 2
<=> 4x = 10
<=> x = \(\dfrac{5}{2}\) (thỏa mãn)
TH2: x - 2 = -(8 - 3x)
<=> x - 2 = -8 + 3x
<=> -2 + 8 = 3x - x
<=> 6 = 2x
<=> x = 3 (thỏa mãn)
b, 5 - |x - 1| = 4
<=> |x - 1| = 1
<=> \(\left[{}\begin{matrix}x-1=1\\x-1=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=0\end{matrix}\right.\) (thỏa mãn)
@Nguyễn Hoàng Vũ
2. 5.(x - 2) - 4.(1 - 3x) = |3 - 7| + 2.(1 + 2x)
<=> 5x - 10 - 4 + 12x = 4 + 2 + 4x
<=> 17x - 14 = 6 + 4x
<=> 17x - 4x = 6 + 14
<=> 13x = 20
<=> x = \(\dfrac{20}{13}\) (thỏa mãn)
@Nguyễn Hoàng Vũ
\(\dfrac{x}{\left(x+1\right)\left(x+4\right)}+\dfrac{x}{\left(x+4\right)\left(x+7\right)}+\dfrac{x}{\left(x+7\right)\left(x+10\right)}=\dfrac{x}{\left(x+1\right)\left(x+10\right)}\left(x\notin\left\{-1;-4;-7;-10\right\}\right)\\ \Leftrightarrow x\left[\dfrac{1}{\left(x+1\right)\left(x+4\right)}+\dfrac{1}{\left(x+4\right)\left(x+7\right)}+\dfrac{1}{\left(x+7\right)\left(x+10\right)}\right]=\dfrac{x}{\left(x+1\right)\left(x+10\right)}\\ \Leftrightarrow\dfrac{1}{3}x\left(\dfrac{1}{x+1}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+7}+\dfrac{1}{x+7}-\dfrac{1}{x+10}\right)=\dfrac{x}{\left(x+7\right)\left(x+10\right)}\\ \Leftrightarrow\dfrac{1}{3}x\left(\dfrac{1}{x+1}-\dfrac{1}{x+10}\right)=\dfrac{x}{\left(x+1\right)\left(x+10\right)}\\ \Leftrightarrow\dfrac{1}{3}x\cdot\dfrac{9}{\left(x+1\right)\left(x+10\right)}-\dfrac{x}{\left(x+1\right)\left(x+10\right)}=0\\ \Leftrightarrow\dfrac{3x}{\left(x+1\right)\left(x+10\right)}-\dfrac{x}{\left(x+1\right)\left(x+10\right)}\\ =0\\ \Leftrightarrow\dfrac{2x}{\left(x+1\right)\left(x+10\right)}=0\\ \Leftrightarrow2x=0\\ x=0\left(tm\right)\)