
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(-x^2+2x-5=-\left(x^2-2x+5\right)=-\left(x^2-2x+1+4\right)\)
\(=-\left[\left(x-1\right)^2+4\right]\)
do \(\left(x-1\right)^2\ge0=>\left(x-1\right)^2+4\ge4=>-\left[\left(x-1\right)^2+4\right]\le-4< 0\)
Vậy ko tồn tại..........
b, \(-4x^2+8x-13=-4\left(x^2-2x+\dfrac{13}{4}\right)\)
\(=-4\left[x^2-2x+1+\dfrac{9}{4}\right]=-4\left[\left(x-1\right)^2+\dfrac{9}{4}\right]\le-9< 0\)
vậy....
c, \(\dfrac{-2021}{x^2+2}\) do \(x^2+2>2=>\dfrac{-2012}{x^2+2}< -1006< 0\)
vậy,,,,,,,,,,
d, \(-3x^2+6x-4=-3\left(x^2-2x+\dfrac{4}{3}\right)=-3\left(x^2-2x+1+\dfrac{1}{3}\right)\)
\(=-3\left[\left(x-1\right)^2+\dfrac{1}{3}\right]\le-1< 0\)
vậy...

a: ĐKXĐ: \(x\ge\dfrac{1}{3}\)
b: ĐKXĐ: \(x< \dfrac{15}{2}\)
c: ĐKXĐ: \(x\le0\)

`sqrt(x-5)` có nghĩa khi:
`x-5 ≥0`
`=> x ≥5`
Vậy `x≥5` thì `sqrt(x-5` có nghĩa
____________
`1/(sqrt(3x-2))` có nghĩa khi
`1/(sqrt(3x-2)) ≥0`
`⇒ 3x-2≥0`
` ⇒3x≥2`
` ⇒x≥2/3`
Vậy `x ≥2/3` thì `1/(sqrt(3x-2))` có nghĩa
Nếu x = 2/3 thì mẫu bằng 0 vậy biểu thức vẫn không có nghĩa thế bài làm vậy là đúng à

Bài 12:
Để N là số nguyên thì \(\sqrt{x}+3⋮\sqrt{x}+5\)
\(\Leftrightarrow-2⋮\sqrt{x}+5\)
\(\Leftrightarrow\sqrt{x}+5\in\left\{1;-1;2;-2\right\}\)(vô lý
Bài 11:
Để M là số nguyên thì \(3\sqrt{x}+1⋮\sqrt{x}+3\)
\(\Leftrightarrow\sqrt{x}+3\in\left\{1;-1;2;-2;4;-4;8;-8\right\}\)
\(\Leftrightarrow\sqrt{x}+3\in\left\{4;8\right\}\)
\(\Leftrightarrow x\in\left\{1;25\right\}\)

1: ĐKXĐ: 3x^2-x+2>=0
=>x thuộc R
2: ĐKXĐ: x>=0 và căn x-1<>0 và 2-căn x<>0 và 2x+1>0 và x<>0
=>x>0 và x<>1 và x<>4

\(a,ĐK:\dfrac{-5}{x^2+6}\ge0\Leftrightarrow x\in\varnothing\)
( Do \(-5< 0;x^2+6>0\Leftrightarrow\dfrac{-5}{x^2+6}< 0,\forall x\))
\(b,ĐK:\dfrac{3x-2}{\left(x-1\right)^2+3}\ge0\\ \Leftrightarrow3x-2\ge0\left[\left(x-1\right)^2+3>0\right]\\ \Leftrightarrow x\ge\dfrac{2}{3}\)
a) ĐKXĐ: \(x^2+6< 0\left(VLý.do.x^2+6\ge6>0\right)\)
Vậy biểu thức k xác định với mọi x
b) \(\sqrt{\dfrac{3x-2}{x^2-2x+4}}=\sqrt{\dfrac{3x-2}{\left(x-1\right)^2+3}}\)
ĐKXĐ: \(\left\{{}\begin{matrix}3x-2\ge0\\\left(x-1\right)^2+3\ne0\left(đúng\forall x\right)\end{matrix}\right.\)
\(\Leftrightarrow x\ge\dfrac{2}{3}\)

a) Ta có: \(P=\dfrac{3x+\sqrt{9x}-3}{x+\sqrt{x}-2}-\dfrac{\sqrt{x}+1}{\sqrt{x}+2}+\dfrac{\sqrt{x}-2}{1-\sqrt{x}}\)
\(=\dfrac{3x+3\sqrt{x}-3-x+1-x+4}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{x+3\sqrt{x}+2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
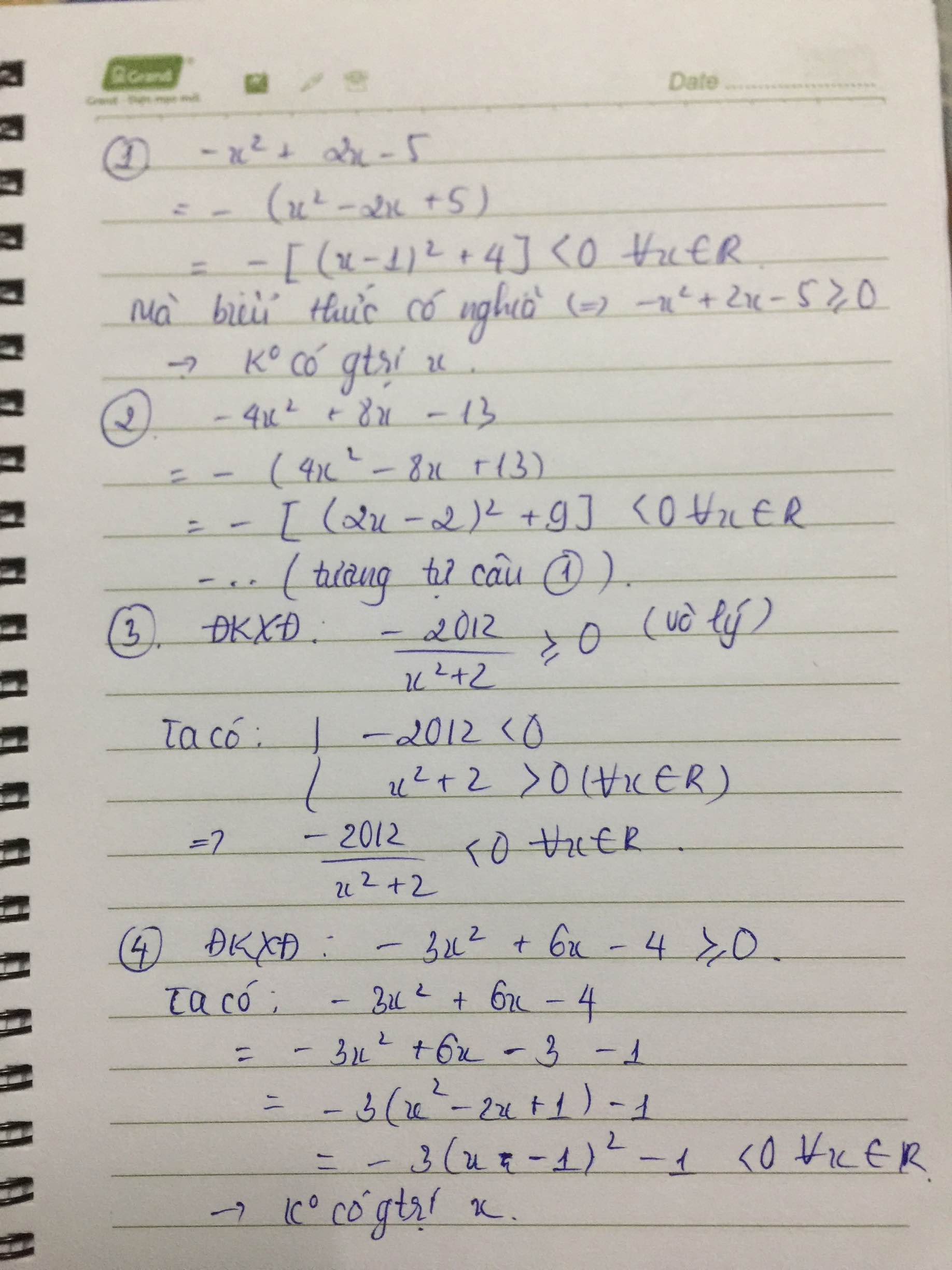
Để biểu thức tồn tại thì \(-\dfrac{5}{3x+2}\ge0\) mà \(-5< 0\Rightarrow3x+2< 0\Rightarrow x< -\dfrac{2}{3}\)
Để biểu thức đã cho tồn tại
`<=>(-5)/(3x+2)>=0`
`=>3x+2<0` ( vì `-5<0` )
`<=>x<-2/3`