Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có hệ phương trình:
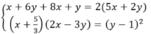
Từ đó ta suy ra
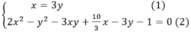
Thế (1) vào (2) ta được: 8y2+7y-1=0⇒y=-1 hoặc y=1/8
Do y < 0 , ta được y = -1, x = -3
Đáp án B

5x-y;2x+1;x-y lập thành cấp số cộng nên
5x-y+x-y=2(2x+1)
=>6x-2y=4x+2
=>2x-2y=2
=>x-y=1
=>y=x-1
\(3;\sqrt{2x+y};x+1\) lập thành cấp số nhân thì \(\left(\sqrt{2x+y}\right)^2=3\left(x+1\right)\)
=>\(2x+y=3x+3\) hoặc -2x-y=3x+3
=>2x+x-1=3x+3 hoặc -2x-x+1=3x+3
=>-1=3(loại) hoặc -3x+1=3x+3
=>-6x=2
=>x=-1/3
=>y=-1/3-1=-4/3
Thử lại, ta sẽ thấy: 2x+y=-2/3-4/3=-6/3=-2<0
=>\(\sqrt{2x+y}\) không có giá trị
Vậy: Không có cặp số (x,y) nào thỏa mãn đề bài

Chọn B
Ta có 8= 2. 4 nên công bội q = 4
Do đó, x = 2.q2 = 2. 42 = 32

Đáp án C
Ba số: 1 − x ; x 2 ; 1 + x lập thành một cấp số cộng khi và chỉ khi:
x 2 = 1 − x + 1 + x 2
⇔ 2 x 2 = 2 ⇔ x = ± 1

Chọn A
+ Ba số x + 6 y ,5 x + 2 y ,8 x + y lập thành cấp số cộng nên
x + 6 y + 8 x + y = 2 5 x + 2 y ⇔ 9 x + 7 y = 10 x + 4 y ⇔ x = 3 y
+ Ba số x + 5 3 , y − 1,2 x − 3 y lập thành cấp số nhân nên x + 5 3 2 x − 3 y = y − 1 2 .
Thay x= 3y vào ta được :
3 y + 5 3 2.3 y − 3 y = y − 1 2 ⇔ 3 y + 5 3 .3 y = y 2 − 2 y + 1 ⇔ 9 y 2 + 5 y − y 2 + 2 y − 1 = 0
⇔ 8 y 2 + 7 y − 1 = 0 ⇔ y = − 1 hoặc y = 1 8 .
Với y= -1 thì x= - 3; với y = 1 8 thì x = 3 8 .

Chọn B
Vì 2 x - 1 ; x ; 2 x + 1 theo thứ tự lập thành cấp số nhân nên
![]()
![]()

Ba số \(2x-1;x;2x+1\) là một cấp số nhân khi:
\(\left(2x-1\right)\left(2x+1\right)=x^2\)
\(\Leftrightarrow\left(2x\right)^2-1^2=x^2\)
\(\Leftrightarrow4x^2-1=x^2\)
\(\Leftrightarrow4x^2-x^2=1\)
\(\Leftrightarrow3x^2=1\)
\(\Leftrightarrow x^2=\dfrac{1}{3}\)
\(\Leftrightarrow x=\pm\sqrt{\dfrac{1}{3}}\)
\(\Leftrightarrow x=\pm\dfrac{\sqrt{3}}{3}\)
Vậy \(2x-1;x;2x+1\) là một cấp số nhân khi \(x=\pm\dfrac{\sqrt{3}}{3}\)

Chọn A
Theo giả thiết ta có :
y = x q ; z = x q 2 x + 3 z = 2 2 y ⇒ x + 3 x q 2 = 4 x q ⇒ x 3 q 2 − 4 q + 1 = 0 ⇔ x = 0 3 q 2 − 4 q + 1 = 0 .
Nếu x = 0 ⇒ y = z = 0 ⇒ công sai của cấp số cộng: x ; 2y ; 3z bằng 0 (vô lí).
nếu
3 q 2 − 4 q + 1 = 0 ⇔ q = 1 q = 1 3 ⇔ q = 1 3 q = 1 .

Theo giả thiết ta có x + 6 y + 8 x + y = 2 5 x + 2 y x − 1 x − 3 y = y + 2 2
⇔ x = 3 y 3 y − 1 3 y − 3 y = y + 2 2 ⇔ x = 3 y 0 = y + 2 2 ⇔ x = − 6 y = − 2 .
Suy ra x 2 + y 2 = 40.
Chọn đáp án A.
Để \(3;x-2;27\) là một cấp số nhân thì:
\(\left(x-2\right)^2=3\cdot27\)
\(\Leftrightarrow\left(x-2\right)^2=81\)
\(\Leftrightarrow\left(x-2\right)^2=9^2\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=9\\x-2=-9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-7\end{matrix}\right.\)
Vậy: \(3;x-2;27\) là cấp số nhân khi \(\Leftrightarrow\left[{}\begin{matrix}x=11\\x=-7\end{matrix}\right.\)
\(3.n^2=27\\ \Leftrightarrow n^2=\dfrac{27}{3}=9=3^2=\left(-3\right)^2\\ \Leftrightarrow\left[{}\begin{matrix}n=3\\n=-3\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x-2=3.3\\x-2=3.\left(-3\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2=9\\x-2=-9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=11\\x=-7\end{matrix}\right.\)