SC
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8 2021
Ta có: \(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+\dfrac{1}{5\cdot7}+...+\dfrac{1}{x\left(x+2\right)}=\dfrac{20}{41}\)
\(\Leftrightarrow\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{x\left(x+2\right)}=\dfrac{40}{41}\)
\(\Leftrightarrow1-\dfrac{2}{x+2}=\dfrac{40}{41}\)
\(\Leftrightarrow\dfrac{2}{x+2}=\dfrac{1}{41}\)
Suy ra: x+2=82
hay x=80
T
0
8 tháng 4 2016
=1/2*(1-1/3+1/3-1/5+....+1/x+1/x+2)
=1/2*(1-1/x+2)
=>1/2*x+1/x+2=20/21
Đến đó đưa về giống tìm x nha
LD
6
13 tháng 8 2019
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{x\left(x+2\right)}=\frac{20}{41}\)
\(\Leftrightarrow1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}=\frac{20}{41}\)
\(\Leftrightarrow1-\frac{1}{x+2}=\frac{21}{41}\)
\(\Leftrightarrow\frac{1}{x+2}=1-\frac{21}{41}\)
\(\Leftrightarrow\frac{1}{x+2}=\frac{20}{41}\)
\(\Leftrightarrow20\left(x+2\right)=41\)
\(\Leftrightarrow x-2=\frac{41}{20}\)
\(\Leftrightarrow x=\frac{41}{20}+2\)
\(\Leftrightarrow x=\frac{81}{20}\)
S
13 tháng 8 2019
\(\frac{1}{1.3}+...+\frac{1}{a\left(a+2\right)}=\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+....+\frac{2}{a\left(a+2\right)}\right)=\frac{1}{2}\left(1-\frac{1}{3}+....-\frac{1}{a+2}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{a+2}\right)=\frac{20}{41}\Rightarrow a+2=41\Leftrightarrow a=39\)
RL
6 tháng 4 2018
Ta có :
\(\dfrac{1}{2}\)(\(\dfrac{1}{1}\)-\(\dfrac{1}{3}\)+\(\dfrac{1}{3}\)-\(\dfrac{1}{5}\)+\(\dfrac{1}{5}\)-\(\dfrac{1}{7}\)+...+\(\dfrac{1}{x}\)-\(\dfrac{1}{x+2}\))=\(\dfrac{20}{41}\)
\(\dfrac{1}{2}\)(\(\dfrac{1}{3}\)-\(\dfrac{1}{x+2}\))=\(\dfrac{20}{41}\)
\(\dfrac{1}{3}\)-\(\dfrac{1}{x+2}\)=\(\dfrac{40}{41}\)
\(\dfrac{1}{x+2}\)=\(\dfrac{1}{3}\)-\(\dfrac{40}{41}\)
CB
0
M
1
18 tháng 3 2016
Gọi \(A=\frac{1005}{2011}\)
A=1/3 + 1/3.5 + 1/5.7 +...............+1/x.(x+2)
A=1/1.3 + 1/3.5 + 1/5.7 +...............+1/x.(x+2)
A . 2=2/1.3 + 2/3.5 + 2/5.7 +......................+2/x.(x+2)
A . 2=1/1-1/3+1/3-1/5+1/5-1/7+..............+1/x-1/x+2
A . 2=1/1+(1/3-1/3)+(1/5-1/5)+..............+(1/x-1/x)-1/x+2
A . 2=1/1-1/x+2
Suy gia:1005/2011 . 2=1/1-1/x+2
2010/2011 =1/1-1/x+2
1/x+2 =1/1-2010/2011
1/x+2 =1/2011
Suy gia:x+2=2011
x =2011-2
x =2009
19 tháng 2 2017
a) Ta có
1/1 - 1/3 + 1/3 - 1/5 + 1/5 - 1/7 + ... + 1/x - 1/x + 2 = 5
rút gọn ta được : 1 - 1/x+2 = 5
<=> x + 2 - 1 / x+ 2
<=> x + 1 / x + 2 = 5
<=> x+ 1 = 5x + 10
<=> - 4x = 9
<=> x = -9/4
B) / x +4/ = 2^0 + 1 ^ 2013
=> /x + 4/ = 1 + 1
=> / x + 4 / = 2
TH 1 : x+ 4 = 2
=> x = 2 - 4 = -2
TH2 : x + 4 = -2
=> x = -2 - 4 = -6
=> x = { - 2 , -6 }
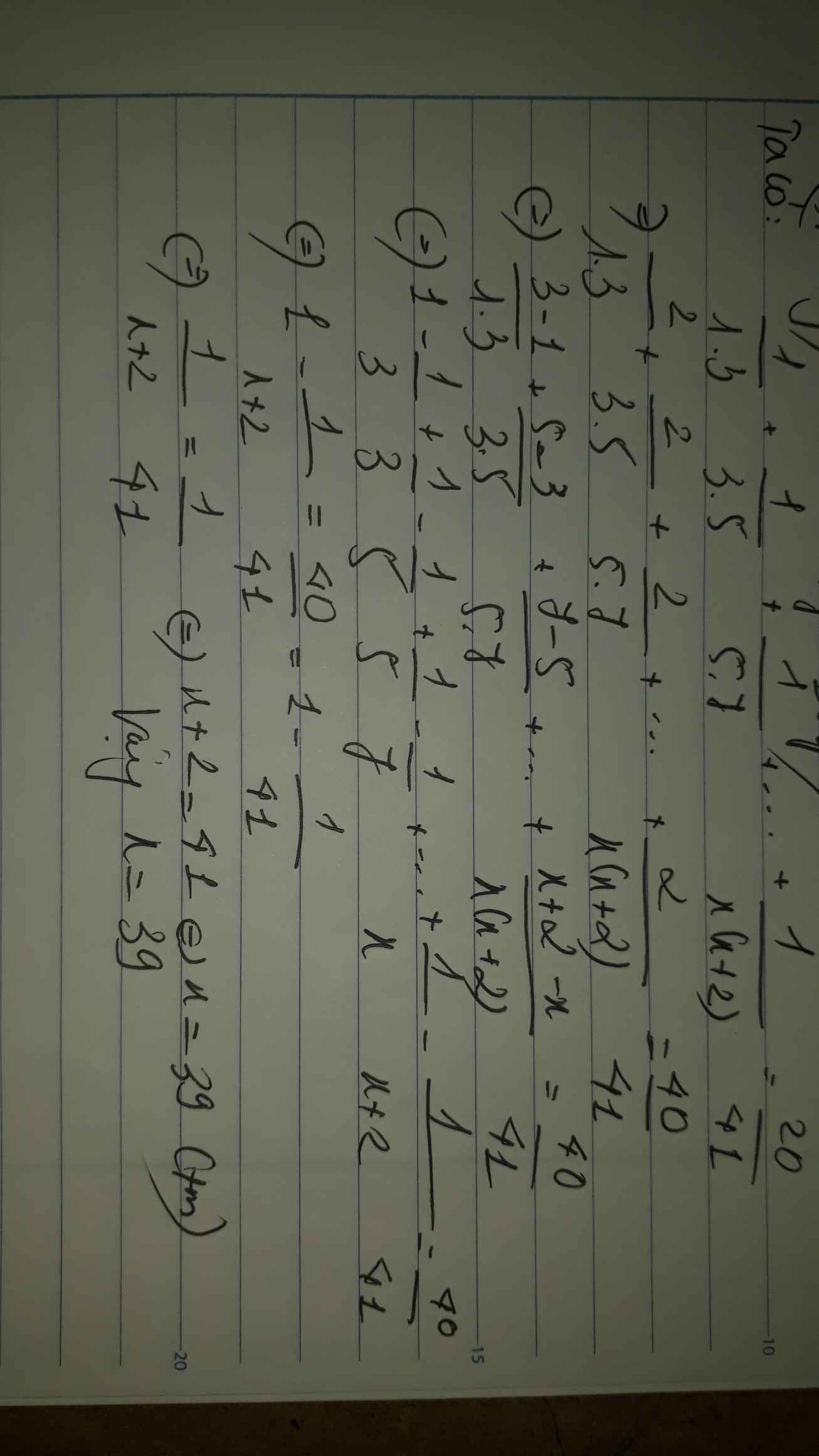
\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{x\left(x+2\right)}=\frac{20}{41}\)
\(\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{x\left(x+2\right)}\right)=\frac{20}{41}\)
\(\frac{1}{2}\left(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{x}-\frac{1}{x+2}\right)=\frac{20}{41}\)
\(\frac{1}{2}\left(1-\frac{1}{x+2}\right)=\frac{20}{41}\)
\(\frac{1}{2}.\frac{x+1}{x+2}=\frac{20}{41}\)
\(\frac{x+1}{x+2}=\frac{20}{41}:\frac{1}{2}\)
\(\frac{x+1}{x+2}=\frac{40}{41}\)
\(x+1=40 \)
\(x=40-1\)
\(x=39\)
Đúng thì ****
Lương Hồ Khánh Duy trả lời đúng nhưng đúng cảu bài khác
Ở đây, câu hỏi ghi x+1 bn ghi x+2