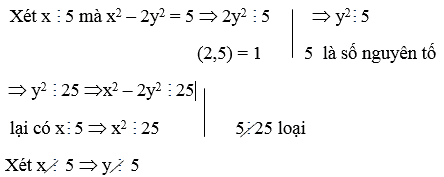NK
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
JK
24 tháng 7 2019
a, x : (-1/2)^3 = -1/2
=> x : (-1/8) = -1/2
=> x = 4
vậy_
b, (3/4)^5.x = (3/4)^7
=> x = (3/4)^7 : (3/4)^5
=> x = (3/4)^2
=> x = 9/16
vậy-
c, (3/5)^8 : x = (-3/5)^6
=> (3/5)^8 : x = (3/5)^6
=> x = (3/5)^8 : (3/5)^6
=> x = (3/5)^2
=> x= 9 /25
NB
2
A
22 tháng 3 2020
a) \(3\left(2x-1\right)+1=\left(-2\right)^2-3\left(-2\right)^3\)
\(\Leftrightarrow6x-3+1=4+24\)
\(\Leftrightarrow6x=4+24-1+3\)
\(\Leftrightarrow6x=30\)
\(\Leftrightarrow x=5\)
b) \(\left(x-2\right)\left(x+3\right)>0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2>0\\x+3>0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x>2\\x>-3\end{cases}}\)
c) \(x^2\left(x+2\right)-9\left(x+2\right)=0\)
\(\Leftrightarrow\left(x^2-9\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-9=0\\x+2=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=\pm3\\x=-2\end{cases}}\)
1 tháng 1 2016
a)Đặt x^3+x^2=0
<=> x^2(x+1)=0
<=>x=0;x=-1
Vậy, nghiệm của đa thức x^3+x^2 là x=0;x=-1
b)Đặt x^3+x^2+x+1=0
<=> x^2(x+1)+(x+1)=0
<=>(x^2+1)(x+1)=0
<=>x^2=-1(vô lí vì x^2>0 với mọi x); x=-1
Vậy đa thức có nghiệm x=-1
HH
22 tháng 7 2019
1) Tìm số nguyên x, biết :
a) 3x = 94/ 273
3x = 1/3
3x = 3-1
=> x = -1
b) 3x = 98 / 273 . 812
3x = 37.38
3x = 315
=> x = 15
c) 2x - 3 / 410 = 83
2x - 3 = 83.410
2x - 3 = 226
=> x - 3 = 26
=> x = 29
d) 22x - 3 / 410 = 83 . 165
22x - 3 / 410 = 269
22x - 3 = 269 . 410
22x - 3 = 289
=> 2x - 3 = 89
2x = 91
x = 91/2
e) 35 / 3x = 310
3x = 35 : 310
3x = 3-5
=> x = -5
K
28 tháng 12 2018
16: Tìm nghiệm nguyên của phương trình
x2 –xy + y2 = 3
Hướng dẫn:
Ta có x2 –xy + y2 = 3 ⇔ (x- 
)2 = 3 – 
Ta thấy (x- )2 = 3 – ≥ 0
⇒ -2 ≤ y ≤ 2
⇒ y= ± 2; ±1; 0 thay vào phương trình tìm x
Ta được các nghiệm nguyên của phương trình là :
(x, y) = (-1,-2), (1, 2); (-2, -1); (2,1) ;(-1,1) ;(1, -1)
T
6 tháng 11 2018
a)\(A=x^2-1\)
\(Nx:\)\(x^2\ge0\)
\(\Rightarrow A_{Min}=0-1=-1\Leftrightarrow x=0\)
b) \(B=x^2-2x+3\)
\(=x\left(x-2\right)+3\)
\(Nx:x\left(x-2\right)\ge0\)
\(\Rightarrow B_{Min}=3\Leftrightarrow x\left(x-2\right)=0\Leftrightarrow x=0\)
c) \(C=\left|2x+1\right|-5\)
\(Nx:\left|2x+1\right|\ge0\Rightarrow2x+1=0\Leftrightarrow2x=-1\Leftrightarrow x=\frac{-1}{2}\)
\(\Rightarrow C_{Min}=-5\Leftrightarrow x=\frac{-1}{2}\)
d) \(D=3x^2+6x-7\)
\(=3\left(x^2+2x\right)-7\)
\(Nx:Min_{x^2+2x}=-1\Leftrightarrow x=-1\)
\(D_{Min}=-8\Leftrightarrow x=-1\)
16 tháng 6 2020
Cái này có cái VD : x(8 + x^2) nên nó có vẻ hơi bị trìu tượng 1 chút.
Ta có : \(M\left(x\right)=x^3\left(9x^2-1\right)-4x\left(x-1\right)+9x^5-4x^2+7+3x^4\)
\(=9x^5-4x^3-4x^2-4x+9x^5-4x^2+7+3x^4\)
\(=18x^5-4x^3-8x^2-4x+7+3x^4\)
\(N\left(x\right)=10x^2+5x^3-3x^3\left(x+1\right)-x\left(8+x^2\right)+8x-7\)
\(=10x^2+5x^3-3x^4+3x^3-8x-x^3+8x-7\)
\(=10x^2+7x^3-3x^4-7\)