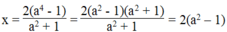PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 11 2016
em gửi bài qua fb thầy chữa cho nhé, tìm fb của thầy bằng sđt: 0975705122 nhé.
24 tháng 5 2022
a: \(\Leftrightarrow x\left(a^2+2\right)=2a^4-2\)
\(\Leftrightarrow x=\dfrac{2\left(a^4-1\right)}{a^2+2}\)
b: \(a^2x+3ax+9=a^2\)
\(\Leftrightarrow x\left(a^2+3a\right)=a^2-9\)(1)
Trường hợp 1: a=-3
=>Pt (1) có vô số nghiệm
Trường hợp 2: a=0
=>Pt (1) vô nghiệm
TRường hợp 3: \(a\notin\left\{-3;0\right\}\)
=>Pt(1) có nghiệm duy nhất là \(x=\dfrac{\left(a-3\right)\left(a+3\right)}{a\left(a+3\right)}=\dfrac{a-3}{a}\)
19 tháng 10 2019
c) Cách 1:
x^4+3x^3-x^2+ax+b x^2+2x-3 x^2+x x^4+2x^3-3x^2 - x^3+2x^2+ax+b x^3+2x^2-3x - (a+3)x+b
Để \(P\left(x\right)⋮Q\left(x\right)\)
\(\Leftrightarrow\left(a+3\right)x+b=0\)
\(\Leftrightarrow\hept{\begin{cases}a+3=0\\b=0\end{cases}\Leftrightarrow}\hept{\begin{cases}a=-3\\b=0\end{cases}}\)
Vậy a=-3 và b=0 để \(P\left(x\right)⋮Q\left(x\right)\)
19 tháng 10 2019
a)
2n^2-n+2 2n+1 n-1 2x^2+n - -2n+2 -2n-1 - 3
Để \(2n^2-n+2⋮2n+1\)
\(\Leftrightarrow3⋮2n+1\)
\(\Leftrightarrow2n+1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Leftrightarrow n\in\left\{0;1;-2;-1\right\}\)
Vậy \(n\in\left\{0;1;-2;-1\right\}\)để \(2n^2-n+2⋮2n+1\)
27 tháng 10 2019
x^4 +ax^2+b x^2+3x-10 x^2 x^4+3x^3-10x^2 - -3x^3+(a+10)x^2+b -3x -3x^3-9x^2+10x - (a+19)x^2-10x+b +(a+19) (a+19)x^2+(3a+57)x-(10a+190) - (-3a-67)x+(b+10a+190)
Để \(x^4+ax^2+b\)chia het cho \(x^2+3x-10\)
\(\Leftrightarrow\left(-3a+67\right)+\left(b+10a+190\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}-3a+67=0\\b+10a+190=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}a=\frac{-67}{3}\\b=\frac{100}{3}\end{cases}}\)
Vậy...
( chả biết đúng ko )
a 2 x + x = 2 a 4 - 2 ⇔ x a 2 + 1 = 2 a 4 - 1