K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
1
30 tháng 1
Ta có : \(x^2-2x-1=0
\)
\(\Leftrightarrow \)\((x-1)^2=2\)
\(\Leftrightarrow
\)\(\left[\begin{array}{}
x-1=\sqrt{2}\\
x-1=-\sqrt{2}
\end{array} \right.\)
Đặt P = \(\dfrac{x^6-6x^5+12x^4-8x^3+2015}{x^6-8x^3-12x^2+6x+2015}\)
=\(\dfrac{(x^6-2x^5-x^4)-(4x^5-8x^4-4x^3)+(5x^4-10x^3-5x^2)-(2x^3-4x^2-2x)+(x^2-2x-1)+2016}
{(x^6-2x^5-x^4)+(2x^5-4x^4-2x^3)+(5x^4-10x^3-5x^2)+(4x^3-8x^2-4x)+(x^2-2x-1)+12x+2016}\)
=\(\dfrac{x^4(x^2-2x-1)-4x^3(x^2-2x-1)+5x^2(x^2-2x-1)-2x(x^2-2x-1)+(x^2-2x-1)+2016}
{x^4(x^2-2x-1)+2x^3(x^2-2x-1)+5x^2(x^2-2x-1)+4x(x^2-2x-1)+(x^2-2x-1)+12x+2016}\)
=\(\dfrac{2016}{12x + 2016}\)
=\(\dfrac{2016}{12(x+1)+2004}\)
=\(\dfrac{168}{x+1+167}\)
=\(\left[\begin{array}{}
\dfrac{168}{\sqrt{2}+167}\\
\dfrac{168}{-\sqrt{2}+167}
\end{array} \right.\)
Chú thích: Hình như mẫu là \(-6x\) chứ không phải \(6x
\) bạn ạ. Hay là mình phân tích sai thì cho mình xin lỗi nhé.
19 tháng 6 2018
\(x\left(x-2015\right)+\left(x-2015\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x-2015\right)=0\)
\(\Rightarrow\hept{\begin{cases}x+1=0\\x-2015=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-1\\x=2015\end{cases}}\)
DL
19 tháng 6 2018
\(x\left(x-2015\right)+x-2015=0\)
\(x\left(x-2015\right)+\left(x-2015\right)=\left(x-2015\right)\left(x+1\right)=0\)
TH1 :\(x+1=0\)
\(x=-1\)
TH2 : \(x-2015=0\)
\(x=2015\)
TM
1
10 tháng 7 2016
Ta có / x + 2013 / + / x + 2014 / + / x + 2015 / = 0x
\(=>x+2013+x+2014+x+2015=0\)
\(=>\hept{\begin{cases}x+2013=0\\x+2014=0\\x+2015=0\end{cases}=>\hept{\begin{cases}x=-2013\\x=-2014\\x=-21015\end{cases}}}\)
31 tháng 10 2019
\(x.\left(x-2015\right)-\left(x-2015\right)=0\)
\(\left(x-1\right)\left(x-2015\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-1=0\\x-2015=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=1\\x=2015\end{cases}}\)
BA
31 tháng 10 2019
\(x\cdot\left(x-2015\right)-x+2015=0\)
\(x\cdot\left(x-2015\right)-\left(x-2015\right)=0\)
\(\left(x-2015\right)\cdot\left(x-1\right)=0\)
\(\orbr{\begin{cases}x-2015=0\\x-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=2015\\x=1\end{cases}}}\)
PS
0
DL
0
TM
1
29 tháng 11 2017
\(A=8x^2-4x+\frac{1}{4x^2}+2015\)
\(=\left(4x^2+\frac{1}{4x^2}\right)+\left(4x^2-4x+1\right)+2014\)
\(=\left(4x^2+\frac{1}{4x^2}\right)+\left(2x-1\right)^2+2014\)
Áp dụng bđt AM - GM ta có : \(4x^2+\frac{1}{4x^2}\ge2\sqrt{4x^2.\frac{1}{4x^2}}=2\)
\(\left(2x-1\right)^2\ge0\forall x\)
\(\Rightarrow\left(4x^2+\frac{1}{4x^2}\right)+\left(4x^2-4x+1\right)\ge2\)
\(\Rightarrow A=\left(4x^2+\frac{1}{4x^2}\right)+\left(4x^2-4x+1\right)+2014\ge2016\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}4x^2=\frac{1}{4x^2}\\\left(2x-1\right)^2=0\end{cases}}\) \(\Rightarrow x=\frac{1}{2}\)
Vậy \(A_{min}=2016\) tại \(x=\frac{1}{2}\)
DT
2
2 tháng 1 2016
thay x=7
ta có:7^15-8*7^14+887^13-8*7^12+...-8*7^2+8*7-2015
f(7)=7^15-8.7^14+8.7^13-8.7^12+...
-8.7^2+8.7-5=
= -7^14+8.7^13-8.7^12+...-8.7^2+8.7-5=
=7^13-8.7^12+...-8.7^2+8.7-5=
= -7^12+...-8.7^2+8.7-5=
=...= -7^2+8.7-5=7-5=2
Kết quả là 2
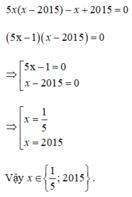
Ta có: \(8x\left(x-2015\right)-x+2015=0\)
\(\Rightarrow8x\left(x-2015\right)-\left(x-2015\right)=0\)
\(\Rightarrow\left(8x-1\right)\left(x-2015\right)=0\)
\(\Rightarrow\orbr{\begin{cases}8x-1=0\\x-2015=0\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{1}{8}\\x=2015\end{cases}}}\)
Vậy \(x=\left\{\frac{1}{8};2015\right\}\)
8x(x - 2015) - (x - 2015) = 0
<=> (8x - 1)(x - 2015) = 0
<=> ........... đến đây thì dễ rồi :))))