
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

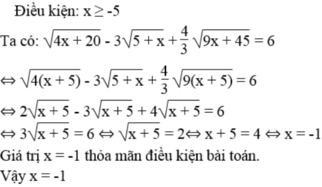

a. \(\Rightarrow2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=6\Rightarrow\sqrt{x+5}\left(2-3+4\right)=6\Rightarrow\sqrt{x+5}=2\Rightarrow x+5=4\Rightarrow x=-1\)
b.\(\Rightarrow5\sqrt{x-1}-\frac{5}{2}\sqrt{x-1}-\sqrt{x-1}=6\Rightarrow\sqrt{x-1}\left(5-\frac{5}{2}-1\right)=6\Rightarrow\sqrt{x-1}=4\Rightarrow x-1=16\Rightarrow x=17\)

1.a) \(\sqrt{x^2-4}-\sqrt{x-2}=0\)
\(\Leftrightarrow\sqrt{\left(x-2\right)\left(x+2\right)}-\sqrt{x-2}=0\)
\(\Leftrightarrow\sqrt{x-2}.\sqrt{x+2}-\sqrt{x-2}=0\)
\(\Leftrightarrow\sqrt{x-2}.\left(\sqrt{x+2}-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x-2}=0\\\sqrt{x+2}-1=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\\sqrt{x+2}=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x+2=1\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}\)
Vậy x=2 hoặc x=-1

\(\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}=16\)
\(\Leftrightarrow4\sqrt{x+1}=16\)
\(\Leftrightarrow\sqrt{x+1}=4\)
<=> x + 1 = 16
<=> x = 15 (nhận)
~ ~ ~
\(\sqrt{4x+20}-3\sqrt{5+x}+\dfrac{4}{3}\sqrt{9x+45}=6\)
\(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=6\)
\(\Leftrightarrow3\sqrt{x+5}=6\)
\(\Leftrightarrow\sqrt{x+5}=2\)
<=> x + 5 = 4
<=> x = - 1 (nhận)

a) \(\sqrt{4-5x}=12\)
ĐK : x ≤ 4/5
Bình phương hai vế
⇔ \(4-5x=144\)
⇔ \(-5x=140\)
⇔ \(x=-28\)( tm )
b) \(\sqrt{1-4x+4x^2}=5\)
⇔ \(\sqrt{\left(1-2x\right)^2}=5\)
⇔ \(\left|1-2x\right|=5\)
⇔ \(\orbr{\begin{cases}1-2x=5\\1-2x=-5\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=3\end{cases}}\)
c) \(\sqrt{4x+20}-3\sqrt{5+x}+\frac{3}{4}\sqrt{9x+45}=6\)
ĐK : x ≥ -5
⇔ \(\sqrt{2^2\left(x+5\right)}-3\sqrt{x+5}+\frac{3}{4}\sqrt{3^2\left(x+5\right)}=6\)
⇔ \(\left|2\right|\sqrt{x+5}-3\sqrt{x+5}+\frac{3}{4}\cdot\left|3\right|\sqrt{x+5}=6\)
⇔ \(2\sqrt{x+5}-3\sqrt{x+5}+\frac{9}{4}\sqrt{x+5}=6\)
⇔ \(\frac{5}{4}\sqrt{x+5}=6\)
⇔ \(\sqrt{x+5}=\frac{24}{5}\)
⇔ \(x+5=\frac{576}{25}\)
⇔ \(x=\frac{451}{25}\)( tm )
d)\(\sqrt{x-2}\le3\)
ĐK : x ≥ 2
⇔ \(x-2\le9\)
⇔ \(x\le11\)
Kết hợp với điều kiện => Nghiệm của bpt là 2 ≤ x ≤ 11

\(dat:\sqrt{x-5}=a\Rightarrow\sqrt{4\left(x-5\right)}+\sqrt{x-5}-\frac{1}{3}=\sqrt{9\left(x-5\right)}\Rightarrow\sqrt{4}.a+a-\frac{1}{3}=\sqrt{9}.a\Rightarrow3a-\frac{1}{3}=3a\left(voli\right)\Rightarrow vonghiem\)
câu a chắc đề như zầy pk bạn???
\(\sqrt{4x-20}+\sqrt{x-5}-\frac{1}{3}+\sqrt{9x-45}=4\)
\(pt\Leftrightarrow2\sqrt{x-5}+\sqrt{x-5}+3\sqrt{x-5}=\frac{13}{3}\)
\(\Leftrightarrow6\sqrt{x-5}=\frac{13}{3}\Rightarrow\sqrt{x-5}=\frac{13}{18}\Leftrightarrow x=\frac{1789}{324}\)
b)đề như này đúng ko bạn??
\(\sqrt{16-32x}-\sqrt{12x}=\sqrt{3x}+\sqrt{9-18x}\)
\(\Leftrightarrow4\sqrt{1-2x}-2\sqrt{3x}=\sqrt{3x}+3\sqrt{1-2x}\)
\(\Leftrightarrow\sqrt{1-2x}-3\sqrt{3x}=0\Leftrightarrow\sqrt{1-2x}=3\sqrt{3x}\)
\(\Leftrightarrow1-2x=27x\Leftrightarrow x=\frac{1}{29}\)
câu c\(\sqrt{4x-20}-3\sqrt{\frac{x-5}{9}}=\sqrt{1-x}\)
Xét điều kiện \(\left\{{}\begin{matrix}x\le1\\x\ge5\end{matrix}\right.\)không tồn tại số nào nằm trong khoảng này
Vậy pt trên vô nghiệm

a: \(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+\dfrac{4}{3}\cdot3\sqrt{x+5}=6\)
\(\Leftrightarrow3\sqrt{x+5}=6\)
=>x+5=4
hay x=-1
b: \(\Leftrightarrow5\sqrt{x-1}-\dfrac{15}{2}\cdot\dfrac{\sqrt{x-1}}{3}-\sqrt{x-1}=6\)
\(\Leftrightarrow\sqrt{x-1}\cdot\dfrac{3}{2}=6\)
\(\Leftrightarrow\sqrt{x-1}=4\)
=>x-1=16
hay x=17

a)
\(\sqrt{25x}=35\)
\(\Leftrightarrow5\sqrt{x}=35\Leftrightarrow\sqrt{x}=7\Leftrightarrow x=49\)
Vậy phương trình đã cho có nghiệm x = 49 .
b)
\(\sqrt{4x+20}-3\sqrt{5+x}+\dfrac{4}{3}\sqrt{9x+45}=6\)
\(\Leftrightarrow2\sqrt{x+5}-3\sqrt{x+5}+4\sqrt{x+5}=6\)
\(\Leftrightarrow3\sqrt{x+5}=6\Leftrightarrow\sqrt{x+5}=2\)
\(\Leftrightarrow x+5=4\Leftrightarrow x=-1\)
Vậy phương trình đã cho có nghiệm là x = -1.

ĐK: \(x\ge0\)\(4\sqrt{x}-2\sqrt{9x}+16\sqrt{x}=5\) 5 (=) \(\sqrt{x}\left(4-2\sqrt{9}+16\right)=5\) (=) \(\sqrt{x}.14=5\)(=) x=\(\frac{25}{196}\)
ĐK: \(x\ge-5\)PT(=) \(\sqrt{5+x}\left(\sqrt{4}-3+\frac{4}{3}.3\right)=6\) (=) \(\sqrt{5+x}.3=6\) (=)\(\sqrt{5+x}=2\)(=) X = -1 (nhận)