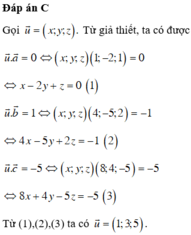
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
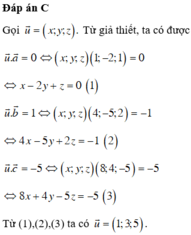
Ta có
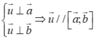
Do
⇔ k = ± 6 2
Mặt khác u ⇀ tạo với tia Oz một góc tù nên
vậy ⇔ k = 6 2
Vậy 6 ; - 6 2 ; 6 2
Chọn đáp án A.
Câu 1.
A = {15;16;17;18;19} (0,25đ)
Câu 2.
a. 2.(72 – 2.32) – 60
= 2.(49 – 2.9) – 60 (0,25đ)
= 2.31 – 60 (0,25đ)
= 62 – 60 = 2 (0,25đ)
b. 27.63 + 27.37
= 27.(63 + 37) (0,25đ)
= 27.100 (0,25đ)
= 2700 (0,25đ)
c. l-7l + (-8) + l-11l + 2
= 7 + (-8) + 11 + 2 (0,5 đ)
= 12 (0,25đ)
d. 568 – 34 {5.l9 – ( 4-1)2l + 10}
= 568 – 34 {5.[9-9] + 10} (0,25đ)
= 568 – 34.10
= 568 – 340 (0,25đ)
= 228 (0,25đ)
Câu 3.
a)2x + 3 = 52 : 5
2x + 3 =5 (0,25đ)
2x = 5-3 (0,25đ)
2x =2 (0,25đ)
x=1 (0,25đ)
b)
105 – ( x + 7) = 27 : 25
105 – ( x + 7) = 22 (0,25đ)
105 – ( x + 7) = 4 (0,25đ)
x + 7 = 105 – 4 (0,25đ)
x + 7 = 101 (0,25đ)
x = 101 – 7 (0,25đ)
x = 94 (0,25đ)
Câu 4.
Gọi x (hs) là số học sinh lớp 6B phải tìm (30<x< 38, x)
Vì hs lớp 6B xếp 2, hàng, 4 hàng, 8 hàng đều vừa đủ nên x⋮2; x⋮4; x⋮8 hay x ∈ BC{2;4;8} (0,25đ)
Ta có: BCNN(2,4,8) = 8 (0,25đ)
⇒ BC(2,4,8) = B(8) ={0; 8; 16;24; 32; 40; …}
Mặt khác: 30<x< 38 (0,25đ)
Nên x = 32
Vậy số học sinh lớp 6B là 32 học sinh (0,25đ)
Câu 5.
Khi M nằm giữa và cách đều hai điểm A và B (0,5đ)
Vẽ được hình có điểm M là trung điểm của AB (0,5đ)
Câu 6.a)
0,25đ
Điểm A nằm giữa O và B (0,25đ)
Vì OA < OB ( 4 < 8 ) (0,25đ)
Ta có: AO + AB = OB
3 + AB = 6 (0,25đ)
AB = 6 -3 = 3 cm (0,25đ)
Vậy OA = AB = 3 cm (0,25đ)
b)
Vì A nằm giữa O, B và cách đều O và B ( OA = AB ) (0,25đ)
Nên A là trung điểm OB (0,25đ)
Bài 2:
a) Ta có:
\(S=1-3+3^2-3^3+3^4-3^5+3^6-3^7+...+3^{96}-3^{97}+3^{98}-3^{99}\)
\(=\left(1-3+3^2-3^3\right)+\left(3^4-3^5+3^6-3^7\right)+...+\left(3^{96}-3^{97}+3^{98}-3^{99}\right)\)
\(=1.\left(1-3+3^2-3^3\right)+3^4.\left(1-3+3^2-3^3\right)+...+3^{96}.\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(1-3+3^2-3^3\right)\)
\(=\left(1+3^4+...+3^{96}\right).\left(-20\right)\) \(\text{⋮}\) \(-20\)
Vậy \(S\) \(\text{⋮}\) \(-20\)
Bài 1:
Ta có:
\(A=\left(5m^2-8m^2-9m^2\right).\left(-n^3+4n^3\right)\)
\(=\left[\left(5-8-9\right).m^2\right].\left[\left(-1+4\right).n^3\right]\)
\(=\left(-12\right).m^2.3.n^3\)
\(=\left(m^2.3\right).\left[\left(-12\right)n^3\right]\)
Xét: \(m^2\ge0\) với V m
3>0 nên \(m^2.3\ge0\) với V m
Như vậy để \(A\ge0\) thì \(\left(-12\right)n^3\ge0\)
-12 < 0 nên nếu \(\left(-12\right)n^3\ge0\) thì \(n^3<0\Rightarrow n<0\)
Vậy với n<0 và mọi m thì \(A\ge0\)
