QT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a)
+) Số trung bình: \(\overline x = \frac{{23.6 + 25.8 + 28.10 + 31.6 + 33.4 + 37.3}}{{6 + 8 + 10 + 6 + 4 + 3}} \approx 28,3\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm,
\(\underbrace {23,...,23}_6,\underbrace {25,...25}_8,\underbrace {28,...,28}_{10},\underbrace {31,...,31}_6,\underbrace {33,...,33}_4,37,37,37\)
Bước 2: \(n = 6 + 8 + 10 + 6 + 4 + 3 = 37\), là số lẻ \( \Rightarrow {Q_2} = {X_{19}} = 28\)
\({Q_1}\) là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\): \(\underbrace {23,...,23}_6,\underbrace {25,...25}_8,\underbrace {28,...,28}_4\)
Do đó \({Q_1} = \frac{1}{2}({X_9} + {X_{10}}) = \frac{1}{2}(25 + 25) = 25\)
\({Q_3}\) là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\)
\(\underbrace {28,...,28}_5,\underbrace {31,...,31}_6,\underbrace {33,...,33}_4,37,37,37\)
Do đó \({Q_3} = \frac{1}{2}({X_9} + {X_{10}}) = \frac{1}{2}(31 + 31) = 31\)
+) Mốt \({M_o} = 28\)
b) Giả sử cỡ mẫu \(n = 10\)
Khi đó ta có bảng số liệu như sau:
Giá trị | 0 | 2 | 4 | 5 |
Tần số | 6 | 2 | 1 | 1 |
+) Số trung bình: \(\overline x = \frac{{0.0,6 + 2.0,2 + 4.0,1 + 5.0,1}}{{0,6 + 0,2 + 0,1 + 0,1}} = 1,3\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm \(0,0,0,0,0,0,2,2,4,5\)
Bước 2: \(n = 10\), là số chẵn \( \Rightarrow {Q_2} = \frac{1}{2}(0 + 0) = 0\)
\({Q_1}\) là trung vị của nửa số liệu: \(0,0,0,0,0\). Do đó \({Q_1} = 0\)
\({Q_3}\) là trung vị của nửa số liệu: \(0,2,2,4,5\). Do đó \({Q_3} = 2\)
+) Mốt \({M_o} = 0\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Sắp xếp lại:
7 9 9 10 10 10 11 12 12 14
Trung vị \({Q_2} = \dfrac{{10 + 10}}{2} = 10\)
Nửa trái \({Q_2}\): 7 9 9 10 10
\({Q_1} = 9\)
Nửa phải: 10 11 12 12 14
\({Q_3} = 12\)
Khoảng tứ phân vị: \({\Delta _Q} = {Q_3} - {Q_1} = 12 - 9 = 3\)
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) Xét mẫu số liệu đã sắp xếp là: \(2;2;5;7;10;10;13;15;19\)
Khoảng biến thiên của mẫu số liệu là: \(R = 19 - 2 = 17.\)
Cỡ mẫu là \(n = 9\) là số lẻ nên giá trị tứ phân vị thứ hai là: \({Q_2} = 10.\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(2;2;5;7\). Do đó \({Q_1} = 3,5\)
Tứ phân vị thứ ba là trung vị của mẫu: \(10;13;15;19\). Do đó \({Q_3} = 14\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 14 - 3,5 = 10,5\)
b) Xét mẫu số liệu đã sắp xếp là: \(1;2;5;5;9;10;10;15;15;19\)
Khoảng biến thiên của mẫu số liệu là: \(R = 19 - 1 = 18.\)
Cỡ mẫu là \(n = 10\) là số chẵn nên giá trị tứ phân vị thứ hai là: \({Q_2} = 9,5.\)
Tứ phân vị thứ nhất là trung vị của mẫu: \(1;2;5;5;9\). Do đó \({Q_1} = 5.\)
Tứ phân vị thứ ba là trung vị của mẫu: \(10;10;15;15;19\). Do đó \({Q_3} = 15\)
Khoảng tứ phân vị của mẫu là: \({\Delta _Q} = 15 - 5 = 10\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
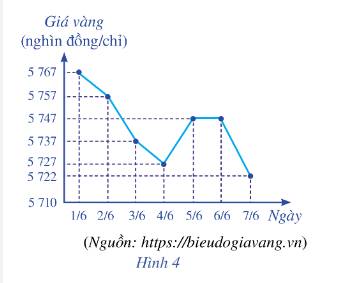
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\)
c) +) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là:
Trung vị của mẫu số liệu: \({Q_2}\) = 5747.
Trung vị của dãy 5722 5727 5737 là: \({Q_1}\) = 5727.
Trung vị của dãy 5747 5757 5767 là: \({Q_3}\) = 5757.
+) Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} ={Q_3} - {Q_1}\) = 5757- 5727= 30.
d) +) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{7} = 5743,43\) ( nghìn đồng/ chỉ)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{7} \approx 219,39\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} = \sqrt {219,39} \approx 14,81\)( nghìn đồng/ chỉ)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5,25 5,42 5,98 6,68 6,21 6,81 7,08 7,02
b)
+) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5,25 5,42 5,98 6,21 6,68 6,81 7,02 7,08
+) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 7,08 - 5,25 = 1,83\)
c)
+) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5,25 5,42 5,98 6,21 6,68 6,81 7,02 7,08
+) Các tứ phân vị của mẫu số liệu là: \({Q_1} = 5,7,{Q_2} = 6,445,{Q_3} = 6,915\)
+) Khoảng tứ phân vị của mẫu số liệu là: \({Q_3} - {Q_1} = 1,215\)
d)
+) Tốc độ tăng trưởng GDP trung bình của Việt Nam giai đoạn 2012 – 2019 là:\(\overline x = \frac{{5,25{\rm{ + }}5,42{\rm{ + }}5,98{\rm{ + }}6,21{\rm{ + }}6,68\; + 6,81{\rm{ + }}7,02{\rm{ + }}7,08}}{8} = 6,30625\) (%)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5,25 - \overline x } \right)}^2} + {{\left( {5,42 - \overline x } \right)}^2} + ... + {{\left( {7,08 - \overline x } \right)}^2}} \right]}}{8} \approx 0,44\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} \approx 0,66\)(%)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
a) \(23;{\rm{ }}41;{\rm{ }}71;{\rm{ }}29;{\rm{ }}48;{\rm{ }}45;{\rm{ }}72;{\rm{ }}41\).
+) Số trung bình: \(\overline x = \frac{{23 + 41 + 71 + 29 + 48 + 45 + 72 + 41}}{8} = 46,25\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \(23;{\rm{ }}29;{\rm{ }}41;{\rm{ }}41;\;{\rm{ }}45;{\rm{ }}48;\;71;72\)
Bước 2: \(n = 8\), là số chẵn nên \({Q_2} = {M_e} = \frac{1}{2}(41 + 45) = 43\)
\({Q_1}\) là trung vị của nửa số liệu \(23;{\rm{ }}29;{\rm{ }}41;{\rm{ }}41\). Do đó \({Q_2} = \frac{1}{2}(29 + 41) = 35\)
\({Q_3}\) là trung vị của nửa số liệu \(45;{\rm{ }}48;\;71;72\). Do đó \({Q_3} = \frac{1}{2}(48 + 71) = 59,5\)
+) Chỉ có giá trị 41 xuất hiện 2 lần, nhiều hơn các giá trị còn lại.
Do đó mốt \({M_o} = 41\)
b) \(12;{\rm{ }}32;{\rm{ }}93;{\rm{ }}78;{\rm{ }}24;{\rm{ }}12;{\rm{ }}54;{\rm{ }}66;{\rm{ }}78\).
+) Số trung bình: \(\overline x = \frac{{12 + 32 + 93 + 78 + 24 + 12 + 54 + 66 + 78}}{9} \approx 49,89\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Bước 1: Sắp xếp mẫu số liệu theo thứ tự không giảm: \(12;{\rm{ }}12;{\rm{ }}24;{\rm{ }}32;{\rm{ }}54;{\rm{ }}66;{\rm{ }}78;{\rm{ }}78;\;93\)
Bước 2: \(n = 9\), là số lẻ nên \({Q_2} = {M_e} = 54\)
\({Q_1}\) là trung vị của nửa số liệu \(12;{\rm{ }}12;{\rm{ }}24;{\rm{ }}32\). Do đó \({Q_2} = \frac{1}{2}(12 + 24) = 18\)
\({Q_3}\) là trung vị của nửa số liệu \(66;{\rm{ }}78;{\rm{ }}78;\;93\). Do đó \({Q_3} = \frac{1}{2}(78 + 78) = 78\)
+) Giá trị 12 và giá trị 78 xuất hiện 2 lần, nhiều hơn các giá trị còn lại.
Do đó mốt \({M_o} = 12,{M_o} = 78.\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Ta có n=2+4+6+12+8+3=35, lẻ.
Trung vị là học sinh thứ 18
Ta thấy 2+4+6<18<2+4+6+12
=> \({Q_2} = 3\)
Ta tìm \({Q_1}\) là trung vị của nửa số liệu bên trái \({Q_2}\)(không bao gồm \({Q_2}\))
Nửa số liệu bên trái \({Q_2}\) có 17 học sinh nên trung vị là học sinh thứ 9:
Ta thấy 2+4<9<2+4+6
=>\({Q_1} = 2\)
Ta tìm \({Q_3}\) là trung vị của nửa số liệu bên phải \({Q_2}\)(không bao gồm \({Q_2}\))
Nửa số liệu bên phải \({Q_2}\) có 17 học sinh nên trung vị là học sinh thứ 9 trong 17 học sinh và là học sinh thứ 9+18=27 trong 35 học sinh.
Ta thấy 2+4+6+12<27<2+4+6+12+8
=>\({Q_3} = 4\)
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Trong mẫu số liệu (1), hiệu giữa số đo lớn nhất và số đo nhỏ nhất là
\(R = {x_{\max }} - {x_{\min }} = 16 - 14 = 2\)
b) +) Sắp xếp các số liệu của mẫu (1) theo thứ tự tăng dần, ta được:
2 5 6 7 8 9 10 11 12 14 16
+) Vậy \({Q_1}{\rm{ }} = 6;{\rm{ }}{Q_2}{\rm{ }} = {\rm{ }}9;{\rm{ }}{Q_3}{\rm{ }} = {\rm{ }}12\) . Suy ra \({Q_3} - {Q_1}{\rm{ = }}12{\rm{ }} - 6 = 6\)
Bước 1: Sắp xếp mẫu số liệu trên theo thứ tự không giảm
11 48 62 81 93 99 127
Bước 2: Trung vị của mẫu số liệu là: 81
Bước 3: Trung vị của dãy số 11 48 62 là: 48
Bước 4: Trung vị của dãy số 93 99 127 là: 99
Bước 5: Vậy \({Q_1} = 48,{Q_2} = 48,{Q_3} = 99\)
*) Biểu diễn tứ phân vị trên trục số: