
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kỳ của (H) luôn thuộc H


- Trong mặt phẳng (P) cho hai đường thẳng Δ và l song song với nhau, cách nhau một khoảng bằng r. Khi quay mặt phẳng (P) xung quanh trục Δ thì đường thẳng l sinh ra một mặt tròn xoay gọi là mặt trụ tròn xoay và được gọi tắt là mặt trụ.
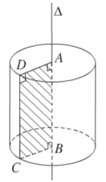
- Hình trụ là hình giới bạn bởi mặt trụ và hai đường tròn bằng nhau, là giao tuyến của mặt trụ và 2 mặt phẳng vuông góc với trục.
Hình trụ là hình tròn xoay khi sinh bởi bốn cạnh của hình một hình chữ nhật khi quay xung quanh một đường trung bình của hình chữ nhật đó.
- Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.
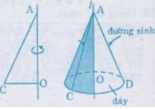
+ Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.
+ Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .
+ A là đỉnh và AO là đường cao của hình nón.



Với hai điểm M và N thuộc khối đa diện thì mọi điểm của đoạn thẳng MN cũng thuộc khối đa diện đó. Ta gọi đó là khối đa diện lồi.
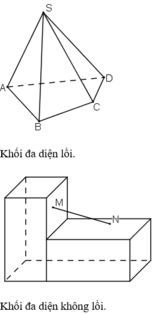
(Hai điểm M, N thuộc khối đa diện nhưng đoạn MN nằm ngoài khối đa diện).

Khối đa diện lồi trong thực tế: kim tự tháp Ai Cập, viên kim cương, rubic
Khối đa diện không lồi trong thực tế: cái bàn

- Khối đa diện (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.
- Ví dụ về hình đa diện không lồi:
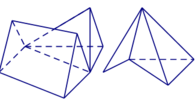

Hai đa diện được gọi là bằng nhau nếu có một phép dời hình biến đa diện này thành đa diện kia.
Ví dụ về đa diện bằng nhau:

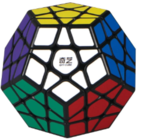
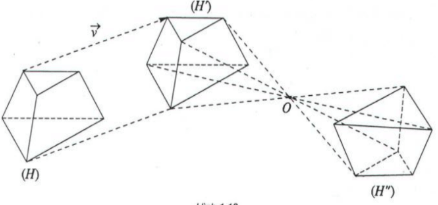
Ví dụ là chiếc Rubik