Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Pt hoành độ:
\(\frac{-x}{2}+3=3x\Leftrightarrow-x+6=6x\Leftrightarrow-x+6-6x=0\)
Giải ra thì \(x=\frac{6}{7}\) . Thế vào lại y = 3x => \(y=\frac{18}{7}\)
Vậy toạ độ giao điểm của 2 đường thẳng trên là (x;y)= (6/7 ; 18/7)
Hoành độ giao điểm là nghiệm của phương trình
\(\frac{-x}{2}+3=3x\)
-x+6 = 6x
6x + x =6
7x=6
x=6/7
y=3.6/7=18/7
Vậy A(6/7; 18/7)

a)Hoành độ giao điểm của (P)và (d) là:
\(\frac{1}{2}x^2=x+4\)
\(\Leftrightarrow x^2=2x+8\)
\(\Leftrightarrow x^2-2x-8=0\)
\(\Leftrightarrow\left(x+2\right).\left(x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\x-4=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=4\end{cases}}}\)
Thay \(x=-2\)vào (d) ta được:
\(y=-2+4=2\)
Thay \(x=4\)vào (d)ta được:
\(y=4+4=8\)
Vậy \(A\left(-2;2\right),B\left(4;8\right)\)hoặc \(A\left(4;8\right),B\left(-2;2\right)\)
b)Mk ko bt làm

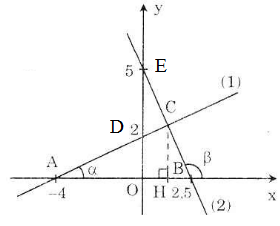
a) * Vẽ đồ thị hàm số y = 0,5x + 2 (1)
Cho x = 0, tính được y = 2 => D(0; 2) thuộc đồ thị.
Cho y = 0, 0 = 0,5.x + 2 => x = -4 => A(-4; 0) thuộc đồ thị. Đường thẳng vẽ qua A, D là đồ thị của (1).
*Vẽ đồ thị hàm số y = 5 – 2x (2)
-Cho x = 0 tính được y = 5 E(0; 5) thuộc đồ thị
-Cho y = 0, 0 = 5 – 2x => x = 2,5 => B(2,5; 0) thuộc đồ thị. Đường thẳng vẽ qua B, E là đồ thị của (2).
b) Ở câu a) ta tính được tọa độ của hai điểm A và B: A(-4; 0), B(2,5; 0)

vt pt hoành độ giao điểm rùi giải pt bậc hai thôi bạn

a/ Tọa độ giao điểm của (P) và (d) là:
\(\frac{x^2}{4}=-\frac{x}{2}+2\Rightarrow x^2=-2x+8\Rightarrow x^2+2x-8=0\Rightarrow\orbr{\begin{cases}x=-4\Rightarrow y=4\\x=2\Rightarrow y=1\end{cases}}\)
Vậy có 2 giao điểm \(\orbr{\begin{cases}A\left(-4;4\right)\\A\left(2;1\right)\end{cases}}\)

a) Vẽ tương đối (d1), (d2)
O y x 6 -4 d1 -1 -3 d2
b) Phương trình hoành độ giao điểm của (d1) và (d2):
\(\frac{3}{2}\)\(x+6\)\(=\) \(-3x-3\)
\(\Leftrightarrow\)\(\frac{9}{2}\)\(x=\)\(-9\)
\(\Leftrightarrow\)\(x=\)\(-2\)
\(\Rightarrow\)\(y=3\)
Vậy giao điểm của (d1) và (d2) là \(\left(-2;3\right)\)
c) Gọi phương trình đường thẳng cần tìm là (d): y = ax + b
(d) // (d1) => (d):\(\frac{3}{2}\) \(x+b\)
A \(\in\)(d2) => A \((\)\(\frac{-4}{3}\)\(;1\)\()\)
Thay tọa độ A vào đường thẳng (d) ta có :
1 = \(\frac{3}{2}\) .\(\frac{-4}{3}\)+ b
\(\Leftrightarrow\)b = 3
Vậy (d): y =\(\frac{3}{2}\) \(x+3\)
:3
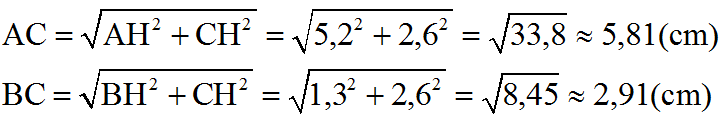

Phương trình hoành độ giao điểm:
\(-\frac{x^2}{2}=3x+4\) \(\Leftrightarrow x^2+6x+8=0\Rightarrow\left[{}\begin{matrix}x=-2\Rightarrow y=-2\\x=-4\Rightarrow y=-8\end{matrix}\right.\)
\(\Rightarrow A\left(-2;-2\right);B\left(-4;-8\right)\)
\(AB=\sqrt{2^2+6^2}=2\sqrt{10}\)