K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NL
24 tháng 4 2017
Vận dụng định lý về tỉ số lượng giác của hai góc phụ nhau ta có:
sin60° = cos(90° – 60°) = cos30°
Tương tự:
cos75° = sin(90° – 75°) = sin 15°
sin52°30′ = cos(90° – 52°30′) = 38°30′
cotg82° = tg8°; tg80° = cotg10°
LH
10

22 tháng 8 2020
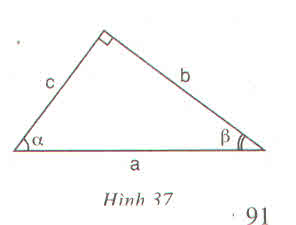
Vẽ \(\Delta\)ABC vuông tại A có B = 75°
=》 C = 90° - 75° = 15°
=》sinB = AC/BC
=> sin75° = AC/BC
=》 cos75° = AB/BC
=》 tan75° = AC/AB
=》 cot75° = AB/AC

sin45=căn 2/2
cos45=căn 2/2
tan 45=1
cot 45=1
Tỉ lượng giác của góc \(45^o\) là:
\(\left\{{}\begin{matrix}sin\left(45^o\right)=\dfrac{\sqrt{2}}{2}\\cos\left(45^o\right)=\dfrac{\sqrt{2}}{2}\\tan\left(45^o\right)=1\\cot\left(45^o\right)=1\end{matrix}\right.\)