
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

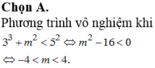


Chọn D
Phương trình 3sinx + mcosx= 5 vô nghiệm khi:
32+ m2 < 52 ↔ m2 < 16 ↔ -4 < m < 4

Do \(m^2-2m+1=\left(m-1\right)^2\ge0>-1;\forall m\) nên phương trình đã cho vô nghiệm khi:
\(m^2-2m+1>1\)
\(\Leftrightarrow m^2-2m>0\)
\(\Rightarrow\left[{}\begin{matrix}m>2\\m< 0\end{matrix}\right.\)

=>(4m-1)*sinx-m*sinx=-8
=>sinx(4m-2)=-8
=>sinx(2m-1)=-4
TH1: m=1/2
PT sẽ là 0*sin x=-4
=>PTVN
TH2: m<>1/2
PT sẽ tương đương với \(sinx=\dfrac{-4}{2m-1}\)
Để phương trình vô nghiệm thì -4/(2m-1)>1 hoặc -4/(2m-1)<-1
=>4/(2m-1)<-1 hoặc 4/(2m-1)>1
=>\(\dfrac{4+2m-1}{2m-1}< 0\) hoặc \(\dfrac{4-2m+1}{2m-1}>0\)
=>\(\dfrac{2m+3}{2m-1}< 0\) hoặc \(\dfrac{2m-5}{2m-1}< 0\)
=>-3/2<m<1/2 hoặc 1/2<m<5/2
Sao thành được sinx(4m-2) thế?
Từ (4m-1)sinx - m.sinx thì lấy sinx làm nhân tử chung thì ra sinx(4m-1-m) = sinx(3m-1) chứ nhỉ?

\(msinx-mcosx=2\)
Phương trình có nghiệm:
\(\Leftrightarrow m^2+\left(-m\right)^2\ge2^2\)
\(\Leftrightarrow2m^2-4\ge0\Rightarrow\)\(\left[{}\begin{matrix}x\le-\sqrt{2}\\x\ge\sqrt{2}\end{matrix}\right.\)
Phương trình vô nghiệm
\(\Leftrightarrow-\sqrt{2}\le x\le\sqrt{2}\)