Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Phương trình có hai nghiệm phân biệt khi \(\Delta'=\left(m+1\right)^2-\left(4m^2-2m-2\right)=-3m^2+4m+3>0\)
\(\Leftrightarrow\dfrac{2-\sqrt{13}}{3}< m< \dfrac{2+\sqrt{13}}{3}\)
b, Yêu cầu bài toán thỏa mãn khi:
\(\left\{{}\begin{matrix}\Delta'>0\\2\left(m+1\right)>0\\4m^2-2m-2>0\end{matrix}\right.\)
\(\Leftrightarrow...\)

Pt đã cho có 2 nghiệm pb khi và chỉ khi:
\(\Delta'=\left(m+1\right)^2-\left(-2m-1\right)>0\)
\(\Leftrightarrow m^2+4m+2>0\)
\(\Rightarrow\left[{}\begin{matrix}m>-2+\sqrt{2}\\m< -2-\sqrt{2}\end{matrix}\right.\)

- Với \(m=\dfrac{1}{2}\Rightarrow\left(x+1\right)^2>0\) có tập nghiệm \(R\backslash\left\{-1\right\}\) thỏa mãn
- Với \(m>\dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-1\\x< -2m\end{matrix}\right.\) hay \(D=\left(-\infty;-2m\right)\cup\left(-1;+\infty\right)\)
Thỏa mãn do \(\left(1;+\infty\right)\subset\left(-1;+\infty\right)\)
- Với \(m< \dfrac{1}{2}\) BPT có nghiệm: \(\left\{{}\begin{matrix}x>-2m\\x< -1\end{matrix}\right.\) hay \(D=\left(-\infty;-1\right)\cup\left(-2m;+\infty\right)\)
Tập nghiệm của BPT chứa \(\left(1;+\infty\right)\) khi:
\(-2m\le1\Rightarrow m\ge-\dfrac{1}{2}\Rightarrow-\dfrac{1}{2}\le m< \dfrac{1}{2}\)
Kết hợp lại ta được: \(m\ge-\dfrac{1}{2}\)

(2m + 1)x + m - 5 ≥ 0 ⇔ (2m + 1)x ≥ 5 - m (*)
TH1: 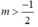 , bất phương trình (*) trở thành:
, bất phương trình (*) trở thành: 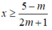
Tập nghiệm của bất phương trình là:
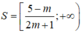
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)
thì (0;1) 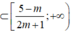
Hay 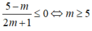
TH2: 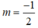 , bất phương trình (*) trở thành:
, bất phương trình (*) trở thành: 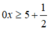
Bất phương trình vô nghiệm. ⇒ không có m .
TH3: Với 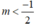 , bất phương trình (*) trở thành:
, bất phương trình (*) trở thành: 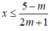
Tập nghiệm của bất phương trình là:
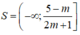
Để bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1)
thì (0;1) 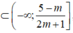
Hay 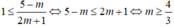
Kết hợp điều kiện 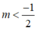 , ⇒ không có m thỏa mãn.
, ⇒ không có m thỏa mãn.
Vậy với m ≥ 5, bất phương trình đã cho nghiệm đúng với ∀x ∈ (0;1).

a/ từ yc đề bài => \(2x^2+\left(m-1\right)x+1-m\ge0\)
nghiệm đúng với mọi x thuộc R
=> \(\Delta\le0\Leftrightarrow\left(m-1\right)^2-4\cdot2\left(1-m\right)\le0\)
\(\Leftrightarrow m^2+2m-7\le0\)
\(\Leftrightarrow m\in\left[-1-2\sqrt{2};-1+2\sqrt{2}\right]\)
b/ x2 - (2m-1)x + 2m-2 = 0
để pt có 2 nghiệm pb => \(\Delta>0\Leftrightarrow\left(2m-1\right)^2-4\left(2m-2\right)>0\)
\(\Leftrightarrow4m^2-12m+9>0\Leftrightarrow\left(2m-3\right)^2>0\Leftrightarrow m\ne\frac{3}{2}\)
=> Gọi 2 nghiệm của pt là x1, x2 (x1<x2)
tập nghiệp của bpt đề cho là: \(S=\left[x_1;x_2\right]\)
theo viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=2m-2\end{matrix}\right.\)
Theo đề ta có: \(\left|x_1-x_2\right|=5\)
\(\Leftrightarrow\left(x_1-x_2\right)^2=25\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=25\)
\(\Leftrightarrow\left(2m-1\right)^2-4\left(2m-2\right)=25\)
\(\Leftrightarrow4m^2-12m-16=0\Leftrightarrow\left[{}\begin{matrix}m=4\\m=-1\end{matrix}\right.\)(tm)
vậy......

Với m=−1m=−1 thì PT f(x)=0f(x)=0 có nghiệm x=1x=1 (chọn)
Với m≠−1m≠−1 thì f(x)f(x) là đa thức bậc 2 ẩn xx
f(x)=0f(x)=0 có nghiệm khi mà Δ′=m2−2m(m+1)≥0Δ′=m2−2m(m+1)≥0
⇔−m2−2m≥0⇔m(m+2)≤0⇔−m2−2m≥0⇔m(m+2)≤0
⇔−2≤m≤0⇔−2≤m≤0
Tóm lại để f(x)=0f(x)=0 có nghiệm thì m∈[−2;0]

a:
\(\text{Δ}=\left(m-1\right)^2-4\left(-2m-1\right)\)
\(=m^2-2m+1+8m+4=m^2+6m+5\)
Để (1) vô nghiệm thì (m+1)(m+5)<0
hay -5<m<-1
Để (1) có nghiệm thì (m+1)(m+5)>=0
=>m>=-1 hoặc m<=-5
Để (1) có hai nghiệm phân biệt thì (m+1)(m+5)>0
=>m>-1 hoặc m<-5
b: Để (1) có hai nghiệm phân biệt cùng dương thì
\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>-1\\m< -5\end{matrix}\right.\\m>1\\m< -\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow m\in\varnothing\)
c. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=m-1\\x_1x_2=-2m-1\end{matrix}\right.\)
\(x_1^2+x_2^2=3\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=3\)
\(\Leftrightarrow\left(m-1\right)^2+2\left(2m+1\right)=3\)
\(\Leftrightarrow m^2+2m=0\Rightarrow\left[{}\begin{matrix}m=0\\m=-2\left(loại\right)\end{matrix}\right.\)

1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)

\(\Leftrightarrow x^2-\left(2m-1\right)x+2m-2=0\) có 2 nghiệm pb \(x_1;x_2\) thỏa mãn \(\left|x_1-x_2\right|=5\)
\(\Delta=\left(2m-1\right)^2-4\left(2m-2\right)=4m^2-12m+9=\left(2m-3\right)^2\)
Pt có 2 nghiệm pb khi \(\left(2m-3\right)^2>0\Rightarrow m\ne\dfrac{3}{2}\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m-1\\x_1x_2=2m-2\end{matrix}\right.\)
\(\left|x_1-x_2\right|=5\Leftrightarrow\left(x_1-x_2\right)^2=25\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=25\)
\(\Leftrightarrow\left(2m-1\right)^2-4\left(2m-2\right)=25\)
\(\Leftrightarrow\left(2m-3\right)^2=25\)
\(\Rightarrow\left[{}\begin{matrix}2m-3=5\\2m-3=-5\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}m=4\\m=-1\end{matrix}\right.\)