Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
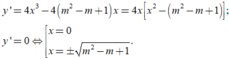
Suy ra đồ thị có hai điểm cực tiểu là A - m 2 - m + 1 ; y C T và B m 2 - m + 1 ; y C T
Khi đó 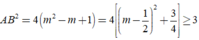
Dấu xảy ra khi m=1/2.
Chọn B.

Chọn C
Ta có y ' = 3 x 2 - 6 m x + 3 ( m 2 - 1 )
Hàm số (1) có cực trị thì PT y ' = 0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nhiệm phân biệt
![]()
Khi đó, điểm cực đại A ( m - 1 ; 2 - 2 m ) và điểm cực tiểu B ( m + 1 ; - 2 m )
Ta có O A = 2 O B ⇔ m 2 + 6 m + 1 = 0
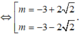

Ta có y’ = 3x2- 6mx + 3( m2-1).
Hàm số đã cho có cực trị thì phương trình y’ =0 có 2 nghiệm phân biệt
⇔ x 2 - 2 m x + m 2 - 1 = 0 có 2 nghiệm phân biệt ⇔ ∆ = 1 > 0 , ∀ m
Khi đó, điểm cực đại A( m-1; 2-2m) và điểm cực tiểu B( m+1; -2-2m)
Ta có
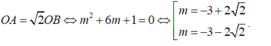
Tổng hai giá trị này là -6.
Chọn C.

Ta có
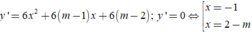
Để hàm số có hai cực trị kh y’=0 có hai nghiệm phân biệt
⇔ 2 - m ≠ - 1 ⇔ m ≠ 3
● Nếu -1<2-m hay m<3,
ycbt 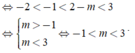
● Nếu 2-m<-1 hay m>3, ycbt
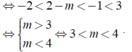
Vậy m ∈ - 1 ; 3 ∪ 3 ; 4
Chọn A.

+ Ta có: y’ = 6x2-6( 2m+1) x+ 6m(m+1)
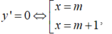
do đó hàm số luôn có cực đại cực tiểu với mọi m.
+ Tọa độ các điểm CĐ, CT của đồ thị là A( m; 2m3+3m2+1 ) và B( m+1; 2m3+3m2)
Suy ra AB = √2 và phương trình đường thẳng AB: x+ y-2m3-3m2-m-1=0.
+ Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
d ( M , A B ) = 3 m 2 + 1 2 ⇒ d ( M , A B ) ≥ 1 2 ⇒ m i n d ( M , A B ) = 1 2
đạt được khi m=0
Chọn B

Chọn B
Ta có:
![]()
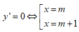
⇒ ∀ m ∈ ℝ , hàm số luôn có CĐ, CT
Tọa độ các điểm CĐ, CT của đồ thị là
![]()
Suy ra A B = 2
và phương trình đường thẳng x + y - 2 m 3 - 3 m 2 - m - 1 = 0
Do đó, tam giác MAB có diện tích nhỏ nhất khi và chỉ khi khoảng cách từ M tới AB nhỏ nhất.
Ta có:
![]()
![]()
⇒ đạt được khi m = 0
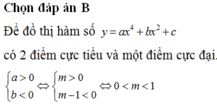
\(y=x^4-2\left(m^2-m+1\right)x+m-1\)
\(y'=4x^3-4\left(m^2-m+1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)
Khoảng cách giữa hai điểm cực tiểu là:
\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)
Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).