NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QA
11 tháng 12 2016
gọi các số cần tìm là n, thương của phép chia n là cho 9 là abc
theo bài ra ta có: n= 9.abc = 9.(a.100+b.10+c)= a.900+b.90+c.9
=> n>a.900 mà a> 1 => a.900>900
=> n>a.900>900
=> n>900
vì n chia hết cho 9 và 5 mà (9,5)=1
=> n chia hết cho 45
=> n=45.k
mà 900<n<1000 => 900< 45.k<1000 => 20<k<23
=> k = 21,22
=> n= 45.k = 945,990
vậy các số cần tìm là 945,990
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Các số tự nhiên nhỏ hơn 1000 gồm các số có 1 chữ số, có 2 chữ số hoặc 3 chữ số.
+ Số có 1 chữ số chia hết cho 5 là: 0 và 5 => có 2 số.
+ Số có 2 chữ số chia hết cho 5:
Hàng đơn vị là 0: chữ số hàng chục có 9 cách chọn.
Hàng đơn vị là 5: chữ số hàng chục có 8 cách chọn (khác 0).
=> Có \(9 + 8 = 17\) (số)
+ Số có 3 chữ số chia hết cho 5:
Hàng đơn vị là 0: chữ số hàng trăm có 9 cách chọn, hàng chục có 8 cách chọn.
Hàng đơn vị là 5: chữ số hàng trăm có 8 cách chọn, hàng chục có 8 cách chọn.
=> Có 9.8+8.8 = 136 (số)
Vậy có tất cả \(2 + 17 + 136 = 155\) số thỏa mãn ycbt.
KC
1
23 tháng 3 2023
Ta có A1 = { 0;2;4;6;8 }
A2 = { 1;3;5;7;9 }
Theo bài ra ta có
TH1 : chọn 5 chữ số abcde tập A1 có
e có 5 cách chọn ; a có 3 cách ; b có 3 cách ; c có 2 cách ; d có 1 cách
-> 90 cách
TH2 : chọn 5 chữ số tập A2 có
a có 5 cách chọn ; b có 4 cách ; c có 3 cách ; d có 2 cách ; e có 1 cách
-> 120 cách
TH3 : chọn 3 chữ số tập A1 ; 2 chữ số tập A2 ta có
\(120.5C3.5C2-24.4C2.5C2=10560\) cách
-> Có tổng 10770 cách
11 tháng 5 2016
Gọi số cần tìm là ab, ta có ab:(a+b)=4 (dư 3)
Ta có: ab=4(a+b)+3=4a+4b+3
10a+b=4a+4b+3
9a=3a+3b+3 (Trừ mỗi vế cho a+b)
9a=3(a+b+1)
3a=a+b+1
2a=b+1
Vì 2a chẵn => b+1 chẵn
\(\Rightarrow\)a là chữ số nên có 10 số a thỏa mãn => có 10 số b thỏa mãn bài toàn. Như vậy có 10 số ab thỏa mãn đáp áp trên
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2023
Không gian mẫu: \(A_6^3=120\)
Gọi số cần lập có dạng \(\overline{abc}\)
Số chia hết cho 5 \(\Rightarrow c=5\) (1 cách chọn)
Chọn và hoán vị cặp ab: \(A_5^2=20\) cách
\(\Rightarrow1.20=20\) số chia hết cho 5
Xác suất: \(P=\dfrac{20}{120}=\dfrac{1}{6}\)
22 tháng 9 2023
\(\overline{34x5y}⋮36\)
\(\left\{{}\begin{matrix}36=4.9\\\left(4;9\right)=1\end{matrix}\right.\)
\(\overline{34x5y}⋮4\Leftrightarrow\left[{}\begin{matrix}y=2\\y=6\end{matrix}\right.\)
- Với \(y=2\)
\(\overline{34x52}⋮9\Leftrightarrow3+4+x+5+2⋮9\)
\(\Leftrightarrow x+14⋮9\)
\(\Leftrightarrow x=4\)
- Với \(y=6\)
\(\overline{34x56}⋮9\Leftrightarrow3+4+x+5+6⋮9\)
\(\Leftrightarrow x+18⋮9\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left\{\left(4;2\right);\left(0;6\right);\left(9;6\right)\right\}\) thỏa mãn đề bài
QT
1
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Gọi số tự nhiên cần tìm là \(\overline {abcd} \).
- Trường hợp 1: \(d = 0\)
Mỗi cách chọn 3 số còn lại (a, b, c) (có xếp thứ tự ) trong 9 số còn lại (1, 2,...,9) là một chỉnh hợp chập 3 của 9.
Số cách chọn 3 chữ số còn lại là \(A_9^3=504\)
- Trường hợp 2: \(d = 5\) .
+ \(a \ne 0,d\) nên a có 8 cách chọn.
+ \(b \ne a,d\) nên b có 8 cách chọn.
+ \(c \ne a,b,d\) nên c có 7 cách chọn.
Vậy có: 504+ 8.8.7= 952 số tự nhiên chia hết cho 5 mà mỗi số có bốn chữ số khác nhau.
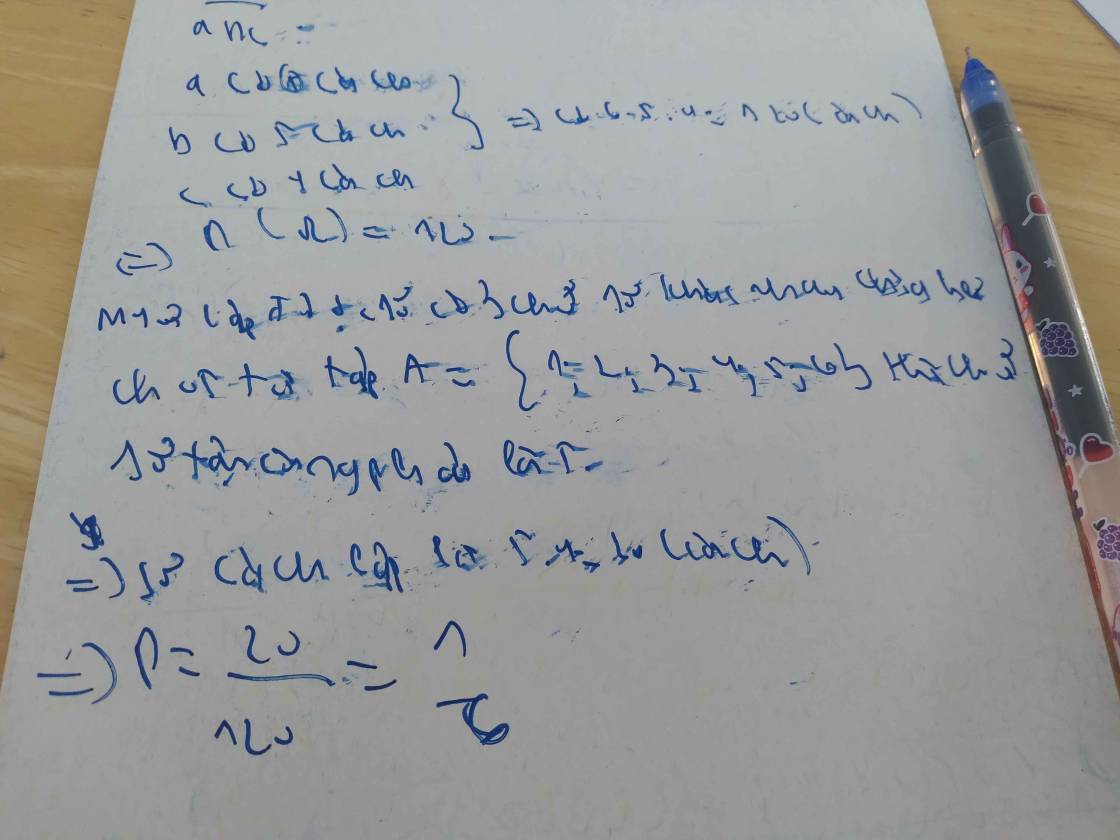
Ta có : 36 = 9 x 4 . Mà ƯC(4;9) = 1
Vậy để chia hết cho 36 thì chia hết cho 4 và 9
Chia hết cho 9 khi 3 + 4 + x + 5 + y9 => 12 + x + y9 (1)
Chia hết cho 4 khi 4 => x = 2 hoặc y = 6
Với y = 2 thay vào (1) => 14 + x9 => x = 4
Với y = 6 thay vào (1) => 18 + x9 => x = 0 hoặc x = 9
Vậy các cặp (x;y) cần tìm là : (4;2), (6;0) và (9;6)