Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Phương pháp:
Sử dụng phương pháp hàm số giải bất phương trình (1), suy ra điều kiện của nghiệm x.
Bất phương trình (2), cô lập m, đưa về dạng m ≥ f(x) trên [a;b] có nghiệm ![]()
Cách giải: ĐK: x ≥ –1
![]()
![]()

Xét hàm số  có
có ![]() => Hàm số đồng biến trên R
=> Hàm số đồng biến trên R
![]()
![]()
Để hệ phương trình có nghiệm thì phương trình (2) có nghiệm ![]()
![]()
![]()
Với ![]()
Để phương trình có nghiệm ![]() (sử dụng MTCT để tìm GTNN)
(sử dụng MTCT để tìm GTNN)

ĐKXĐ:
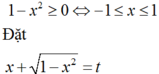
ta có
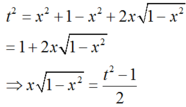
Ta có:
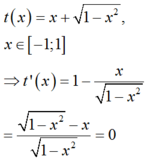
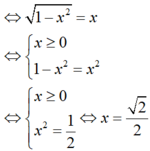
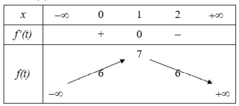
BBT:
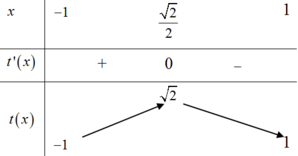
Từ BBT ta có:
t ∈ - 1 ; 2
Khi đó phương trình trở thành:
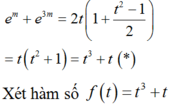
ta có
![]()
Hàm số đồng biến trên R Hàm số đồng biến trên t ∈ - 1 ; 2 .
Từ
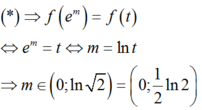
Chọn B.


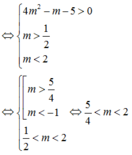

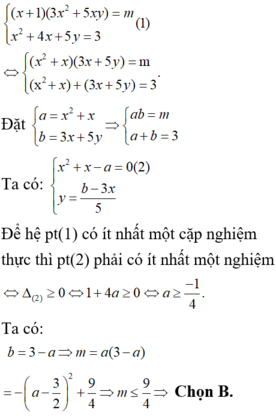
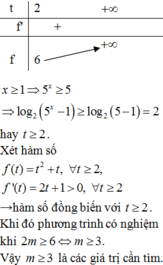




Đáp án B