Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
Phương pháp: Chia cả 2 vế cho 3x, đặt 
, tìm điều kiện của t.
Đưa về bất phương trình dạng 
Cách giải :
Ta có 
Đặt 
, khi đó phương trình trở thành
Ta có: 
Vậy 
giả sử : \(\frac{mx+m}{\left(m+1\right)x-m+2}>0\)\(,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{m.0+m}{\left(m+1\right).0-m+2}>0\) \(\Rightarrow\frac{m}{2-m}>0\)
\(\Rightarrow0\)\(<\)\(m<\)\(2\)
ngược lại \(0<\)\(m<2\) thì:
\(mx+m>0,\text{∀}x\in\left[0;2\right]\)
\(\left(m+1\right)x\ge0>m-2,\)\(\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\left(m+1\right)x-m+2>0,\text{∀}x\in\left[0;2\right]\)
\(\Rightarrow\frac{mx+m}{\left(m+1\right)x-m+2}>0,\text{∀}x\in\left[0;2\right]\)
vậy: \(0\)\(<\)\(m<\)\(2\) là kết quả cần tìm
Đáp án D
B P T ⇔ 2 3 x + m − 1 3 x + m − 1 > 0 ⇔ 2 3 x − 3 x − 1 + m 3 x + 1 > 0 ⇔ m > 3 x − 8 x + 1 3 x + 1 ; ∀ x ∈ ℝ * .
Xét hàm số f x = 3 x − 8 x + 1 3 x + 1 ; ∀ x ∈ ℝ ,
ta có f ' x = 8 x ( ln 3 − ln 8 .3 x − ln 8 3 x + 1 2 < 0 ; ∀ x ∈ ℝ .
Suy ra f x là hàm số nghịch biến trên ℝ mà lim x → − ∞ f x = 1 , do đó min x ∈ ℝ f x = lim x → − ∞ f x = 1
Vậy * ⇔ m ≥ min x ∈ ℝ f x = 1 ⇒ m ≥ 1 là giá trị cần tìm.
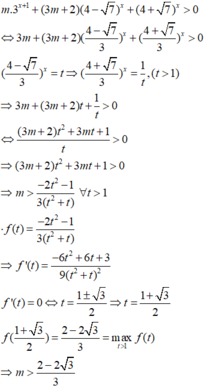
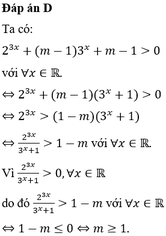
Đáp án D
Ta có log 0 , 02 log 2 3 x + 1 > log 0 , 02 m ⇔ m > log 2 3 x + 1 (vì cơ số = 0,02 < 1)
Xét hàm số f x = log 2 3 x + 1 trên - ∞ ; 0 có f ' x = 3 x . ln 3 3 x + 1 ln 2 > 0 ; ∀ x ∈ - ∞ ; 0
Suy ra f(x) là hàm số đồng biến trên - ∞ ; 0 ⇒ m a x - ∞ ; 0 f x = f 0 = 1
Vậy để bất phương trình có nghiệm ∀ x ∈ - ∞ ; 0 ⇒ m ≥ 1 .