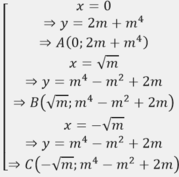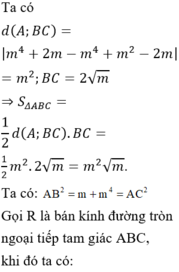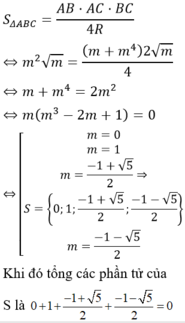Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(y=4x^3-4mx=4x\left(x^2-m\right)=0\Leftrightarrow\begin{cases}x=0\\x^2=m\end{cases}\)
Hàm số đã cho có 3 điểm cực trị <=> phương trình y=0 có 3 nghiệm phân biệt và y đổi dấu khi x đi qua các nghiệm đó <=>m>0
- Khi đó 3 điểm cực trị của đồ thị hàm số là :
\(A\left(0;m-1\right);B\left(-\sqrt{m};-m^2=m-1\right);\left(\sqrt{m};-m^2=m-1\right)\)
- \(S_{ABC}=\frac{1}{2}\left|y_B-y_A\right|.\left|x_C-x_B\right|=m^2\sqrt{m}\); \(AB=AC=\sqrt{m^4+m},BC=2\sqrt{m}\)
- \(R=\frac{AB.AC.BC}{4S_{ABC}}=1\Leftrightarrow\frac{\left(m^4+m\right)2\sqrt{m}}{4m^2\sqrt{m}}=1\)\(\Leftrightarrow m^3-2m+1=0\)
\(\Leftrightarrow\begin{cases}m=1\\m=\frac{\sqrt{5}-1}{2}\end{cases}\)
có 3 điểm cực trị đồng thời các điểm cực trị của đồ thị lập thành tam giác có bán kính đường tròn ngoại tiếp bằng 1. Tính tổng các phần tử của S.
TXĐ: 
.
Ta có 
Để hàm số có 3 điểm cực trị thì phương trình y'=0 có 3 nghiệm phân biệt 
Khi đó ta có:
y' = 0
.
Ta có: 
Gọi R là bán kính đường tròn ngoại tiếp tam giác ABC, khi đó ta có:
Khi đó tổng các phần tử của S là
Chọn C
Đáp án B
Điều kiện để hàm số có 3 cực trị
Ta có y'=4x3-4(m-1)x; y'=0
4x[x2-(m-1)]=0
Điều kiện để hàm số có 3 cực trị thì pt (1) phải có hai nghiệm phân biệt khác 0 tức là
m-1>0
Áp dụng công thức:
Kết hợp điều kiện 
ta có
.
Chọn B
Ta có :
Hàm số đã cho có ba điểm cực trị khi m > 0(*)
Khi đó ba điểm cực trị của đồ thị hàm số là
A ( 0 ; m - 1 ) , B ( - m ; - m 2 + m - 1 )
S ∆ A B C = 1 2 y B - y A x c - x B
Kết hợp điều kiện (*) ta có
[Phương pháp trắc nghiệm]
Áp dụng công thức
Kết hợp điều kiện (*) ta có
Chọn B
Ta có :
Hàm số đã cho có ba điểm cực trị khi m > 0(*)
Khi đó ba điểm cực trị của đồ thị hàm số là
A ( 0 ; m - 1 ) , B ( - m ; - m 2 + m - 1 )
S ∆ A B C = 1 2 y B - y A x c - x B
Kết hợp điều kiện (*) ta có
[Phương pháp trắc nghiệm]
Áp dụng công thức
Kết hợp điều kiện (*) ta có
Ta có \(y=4x^3-4mx=4x\left(x^2-m\right)=0\Leftrightarrow x=0\) hoặc \(x^2=m\)
Hàm số đã cho có 3 điểm cực trị \(\Leftrightarrow\) phương trình y' = 0 có 3 nghiệm phân biệt và y' đổi dấu khi x đi qua các nghiệm đó <=> m > 0. Khi đó 3 điểm cực trị của đồ thị hàm số là :
\(A\left(0;m-1\right);B\left(-\sqrt{m};m^2+m-1\right);C\left(\sqrt{m};-m^2+m-1\right)\)
a) Ta có \(S_{\Delta ABC}=\frac{1}{2}\left|y_B-y_A\right|.\left|y_C-y_B\right|=m^2\sqrt{m}\)
\(AB=AC=\sqrt{m^4+m};BC=2\sqrt{m}\)
\(R=\frac{AB.AC.BC}{4S_{\Delta ABC}}=1\Leftrightarrow\frac{\left(m^4+m\right)2\sqrt{m}}{4m^2\sqrt{m}}=1\)
\(\Leftrightarrow m^3-2m+1=0\Leftrightarrow m=1\) hoặc \(m=\frac{\sqrt{5}-1}{2}\)
Vậy \(m=1;m=\frac{\sqrt{5}-1}{2}\) là giá trị cần tìm
b) Vì B, C đối xứng nhau qua trục tung nên BC luôn vuông góc OA
Do đó O là trực tâm tam giác ABC khi và chỉ khi \(\overrightarrow{OB}.\overrightarrow{AC}=0\)
\(\overrightarrow{OB}\left(-\sqrt{m};-m^2+m-1\right);\overrightarrow{AC}\left(\sqrt{m};-m^2\right)\)
Suy ra \(-m-m^2\left(-m^2+m-1\right)=0\Leftrightarrow m\left(-m^3+m^2-m+1\right)=0\)
\(\Leftrightarrow m\left(m-1\right)\left(m^2+1\right)=0\Leftrightarrow m=0\) hoặc m = 1
Vậy m = 0 hoặc m = 1 là giá trị cần tìm
c) Rõ ràng tam giác ABC cân tại A và truyên tuyến kẻ từ A thuộc Oy. Do đó O là trọng tâm của tam giác ABC
<=> \(y_A+2y_B=0\)
\(\Leftrightarrow m-1+2\left(-m^2+m-1\right)=0\)
\(\Leftrightarrow2m^2-3m+3=0\) vô nghiệm
Vậy không tồn tai giá trị m thỏa mãn yêu cầu bài toán
bn ơi cho mk hỏi cái công thức tính S tam giác ABC=1/2|yB-yA|.|yC-yB| ở đâu vậy ạ
Đáp án B
Tam giác có tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp trùng nhau là tam giác đều.
Bài toán trở thành tìm số các giá trị thực của tham số m để đồ thị hàm số có ba điểm cực trị tạo thành một tam giác đều.
Trong sách Công phá toán 3 tác giả đã đề cập đến công thức tổng quát cho bài toán này.
Để thỏa mãn yêu cầu trên thì b 3 a = − 24 ⇔ − 2 m − 1 3 1 = − 24 ⇔ m − 1 3 = 3 .
Phương trình có duy nhất một nghiệm nên ta chọn B