Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: m(x - 1) < 3 – x
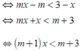
Bất phương trình tương đương là ( m + 1 )x < m + 3
Rõ ràng với m ≠ - 1 thì bất phương trình luôn có nghiệm
Với m = - 1 ta có bất phương trình có dạng: 0x < 2 luôn đúng với mọi x
Vậy bất phương trình có nghiệm với mọi m.
Chọn đáp án C.

ĐKXĐ: \(x\ne1;x\ne-2\)\(\Rightarrow\left(2x-m\right)\left(x+2\right)+\left(x+1\right)\left(x-1\right)=3\left(x-1\right)\left(x+2\right)\Leftrightarrow2x^2+4x-mx-2m+x^2-1=3x^2+3x-6\Leftrightarrow3x^2+4x-mx-2m-3x^2-3x=-6\) \(\Leftrightarrow x-mx=2m-6\Leftrightarrow x\left(1-m\right)=2m-6\Leftrightarrow x=\dfrac{2m-6}{1-m}\)
\(\Rightarrow\) Để pt có nghiệm \(\Leftrightarrow m\ne1\) Vậy...

\(\left\{{}\begin{matrix}m\left(x+3\right)\le x+5\\m\left(x+2\right)\ge x+3\end{matrix}\right.\) có nghiệm chung \(\left(1\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{x+5}{x+3}\\m\ge\dfrac{x+3}{x+2}\end{matrix}\right.\)
Để 2 pt có 1 nghệm chung thì \(\dfrac{x+5}{x+3}=\dfrac{x+3}{x+2}\)
\(\Leftrightarrow\left(x+5\right)\left(x+2\right)-\left(x+3\right)^2=0\)
\(\Leftrightarrow x^2+7x+10-x^2-6x-9=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Thay \(x=-1\) vào \(\left(1\right):\)
\(\left\{{}\begin{matrix}m\left(-1+3\right)\le-1+5\\m\left(-1+2\right)\ge-1+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m\le4\\m\ge2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le2\\m\ge2\end{matrix}\right.\)
\(\Rightarrow m=2\)
Vậy m = 2 thì bpt trên có nghiệm chung

1) Phương trình ban đầu tương đương :
\(\left(2021x-2020\right)^3=\left(2x-2\right)^3+\left(2019x-2018\right)^3\)
Đặt \(a=2x-2,b=2019x-2018\)
\(\Rightarrow a+b=2021x-2020\)
Khi đó phương trình có dạng :
\(\left(a+b\right)^3=a^3+b^3\)
\(\Leftrightarrow3ab\left(a+b\right)=0\)
\(\Leftrightarrow3\cdot\left(2x-2\right)\cdot\left(2019x-2018\right)\cdot\left(2021x-2002\right)=0\)
\(\Leftrightarrow\)Hoặc \(2x-2=0\)
Hoặc \(2019x-2018=0\)
Hoặc \(2021x-2020=0\)
\(\Rightarrow x\in\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\) (thỏa mãn)
Vậy : phương trình đã cho có tập nghiệm \(S=\left\{1,\frac{2018}{2019},\frac{2020}{2021}\right\}\)
\(x\left(2x-3\right)+x\left(x-m\right)=3x^2+x-m\)
\(\Leftrightarrow2x^2-3x+x^2-xm=3x^2+x-m\)
\(\Leftrightarrow-3x-xm=x-m\)
\(\Leftrightarrow4x+xm=m\Leftrightarrow x\left(4+m\right)=m\)
\(\Leftrightarrow x=\frac{m}{m+4}\)
Phương trình có nghiệm không âm \(\Leftrightarrow x\ge0\)
\(\Rightarrow\frac{m}{m+4}\ge0\)
Mà \(m+4>m\)nên \(\orbr{\begin{cases}m\ge0\\m+4\le0\end{cases}}\Leftrightarrow\orbr{\begin{cases}m\ge0\\m\le-4\end{cases}}\)

a: Khi m=1 thì pt sẽ là: x+x-3=6x-6
=>6x-6=2x-3
=>4x=3
=>x=3/4
b: m^2x+m(x-3)=6(x-1)
=>x(m^2+m-6)=-6+3m=3m-6
=>x(m+3)(m-2)=3(m-2)
Để (1) có nghiệm duy nhất thì (m+3)(m-2)<>0
=>m<>-3 và m<>2
=>x=3/(m+3)
\(A=\dfrac{\left(\dfrac{3}{m+3}\right)^2+\dfrac{6}{m+3}+3}{\left(\dfrac{3}{m+3}\right)^2+2}\)
\(=\dfrac{9+6m+18+3m^2+18m+27}{\left(m+3\right)^2}:\dfrac{9+2m^2+12m+18}{\left(m+3\right)^2}\)
\(=\dfrac{3m^2+24m+54}{2m^2+12m+27}>=\dfrac{1}{2}\)
Dấu = xảy ra khi 6m^2+48m+108=2m^2+12m+27
=>4m^2+36m+81=0
=>m=-9/2
Rõ ràng: m 2 + m - 6 ≠ 0 thì bất phương trình luôn có nghiệm
Xét m 2 + m - 6 = 0
Từ hai trường hợp, ta được bất phương trình có nghiệm khi m ≠ 2
Chọn đáp án A.