K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2021
ĐKXĐ:
a. \(\left\{{}\begin{matrix}x-1\ge0\\x-3\ne0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ge1\\x\ne3\end{matrix}\right.\) \(\Rightarrow D=[1;+\infty)\backslash\left\{3\right\}\)
b. \(D=R\)
c. \(x+3>0\Rightarrow x>-3\Rightarrow D=\left(-3;+\infty\right)\)
d. \(\left|x-2\right|\ge0\Rightarrow x\in R\Rightarrow D=R\)
MP
0
NH
1
27 tháng 11 2023
\(y=\sqrt{x+3+2\sqrt{x+2}}+\sqrt{2-x^2+2\sqrt{1-x^2}}\)
\(=\sqrt{x+2+2\sqrt{x+2}+1}+\sqrt{1-x^2+2\cdot\sqrt{1-x^2}\cdot1+1}\)
\(=\sqrt{\left(\sqrt{x+2}+1\right)^2}+\sqrt{\left(\sqrt{1-x^2}+1\right)^2}\)
\(=\left|\sqrt{x+2}+1\right|+\left|\sqrt{1-x^2}+1\right|\)
ĐKXĐ: \(\left\{{}\begin{matrix}x+2>=0\\1-x^2>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=-2\\x^2< =1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>=-2\\-1< =x< =1\end{matrix}\right.\)
=>-1<=x<=1
TXĐ là D=[-1;1]
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
a) \(y = \frac{1}{{{x^2} - x}}\) xác định \( \Leftrightarrow {x^2} - x \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\x \ne 1\end{array} \right.\)
Tập xác định \(D = \mathbb{R}\backslash \left\{ {0;1} \right\}\)
b) \(y = \sqrt {{x^2} - 4x + 3} \) xác định \( \Leftrightarrow {x^2} - 4x + 3 \ge 0 \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\x \le 1\end{array} \right.\)
Tập xác định \(D = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
c) \(y = \frac{1}{{\sqrt {x - 1} }}\) xác định \( \Leftrightarrow x - 1 > 0 \Leftrightarrow x > 1\)
Tập xác định \(D = \left( {1; + \infty } \right)\)
QT
1
HQ
Hà Quang Minh
Giáo viên
23 tháng 9 2023
Tìm tập xác định của hàm số: \(y = \frac{{\sqrt {x + 2} }}{{x - 3}}\) là \(\left\{ \begin{array}{l}x + 2 \ge 0\\x - 3 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 2\\x \ne 3\end{array} \right.\)
Vậy tập xác định của hàm số là \(D = \left[ { - 2; + \infty } \right)\backslash \left\{ 3 \right\}\).
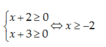
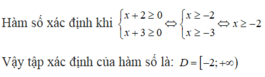
Vậy tập xác định của hàm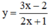
là D = R \ {-1/2}.