K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
4 tháng 9 2023
11:
n^3-n^2+2n+7 chia hết cho n^2+1
=>n^3+n-n^2-1+n+8 chia hết cho n^2+1
=>n+8 chia hết cho n^2+1
=>(n+8)(n-8) chia hết cho n^2+1
=>n^2-64 chia hết cho n^2+1
=>n^2+1-65 chia hết cho n^2+1
=>n^2+1 thuộc Ư(65)
=>n^2+1 thuộc {1;5;13;65}
=>n^2 thuộc {0;4;12;64}
mà n là số tự nhiên
nên n thuộc {0;2;8}
Thử lại, ta sẽ thấy n=8 không thỏa mãn
=>\(n\in\left\{0;2\right\}\)
LT
1
KL
1
YN
16 tháng 12 2021
Answer:
Vì n là số có hai chữ số nên 9 < n < 100 => 18 < 2n < 200
Có: 2n là số chính phương chẵn nên ta có thể nhận giá trị: 36, 64, 100, 144, 196
Trường hợp 1: \(2n=36\Rightarrow n=18\Rightarrow n+4=18+4=22\) (Loại)
Trường hợp 2: \(2n=64\Rightarrow n=32\Rightarrow n+4=32+4=36\) (Thoả mãn)
Trường hợp 3: \(2n=100\Rightarrow n=50\Rightarrow n+4=50+4=54\) (Loại)
Trường hợp 4: \(2n=144\Rightarrow n=72\Rightarrow n+4=72+4=76\) (Loại)
Trường hợp 5: \(2n=196\Rightarrow n=98\Rightarrow n+4=98+4=102\) (Loại)
Vậy số tự nhiên cần tìm là \(32\)
TV
1 tháng 4 2016
a) Một số tự nhiên chẵn có dạng 2k (k(N), khi đó (2k)2 = 4k2 là số chia hết cho 4 còn số tự nhiên lẻ có dạng 2k+1 (k(N) ,
Khi đó (2k+1)2 = 4k2+ 4k +1 là số chia cho 4 dư 1. Như vậy một số chính phương hoặc chia hết cho 4 hoặc chia cho 4 dư 1 , do đó không thể viết đựơc dưới dạng 4n+2 hoặc 4n+3(n(N)
b) Một số tự nhiên chỉ có thể viết dưới dạng 3k hoặc 3k± 1 (k( N)
khi đó bình phương của nó có dạng (3k)2 =9k2 là số chia hết cho 3 ,hoặc có dạng (3k± 1) 2 = 9k2 ± 6k +1 là số khi chia cho 3 thì dư 1.
Như vậy một số chính phương không thể viết dưới dạng 3n+2(n(N) ĐPCM.
HM
1 tháng 4 2016
n là số tự nhiên có 2 chữ số nên 10< hoặc = n <100 do đó 21< hoac bang 2n+1<201
2n+1 là số chính phương lẻ nên 2n+1 chỉ có thể nhận 1 trong các giá trị 25;49;81;121;169
suy ra n chỉ có thể nhận 1 trong các giá trị 12;24;40;60;84
suy ra 3n+1 chỉ có thể nhận 1 trong các giá trị 37;73;121;181;253
Trong các số trên chỉ có số 121=11^2 là 1 số chính phương
Vậy số n tự nhiên có 2 chữ số cần tìm là 40
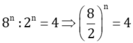
Ta có:
\(64=2^6< 88< 2^7=128\)
Suy ra: \(2^6< 2^n< 2^7\Rightarrow6< n< 7\)
Theo bài ra n là số tự nhiên nên không tồn tại n thõa mãn bài toán.
kết luận:....
n = 44