PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
1
PT
1
CM
19 tháng 4 2019
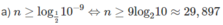
Vì n là số tự nhiên bé nhất nên n = 30.
b) n = 4
c) n = 16
d) n = 15
PT
1
20 tháng 10 2019
a
=>(n+2)=5 :.n+2
=>5:. n+2
=>n+2 E (1,5)
th1
N+2=1
th2 tựlamf
AM
6 tháng 9 2020
Câu 2. Đặt A=x2+y2+1
Nhập \(2^A=\left(A-2x+1\right)4^x\) vào máy tính Casio. Cho x=0.01, tìm A
Máy sẽ giải ra, A=1.02=1+2x
\(\Leftrightarrow x^2+y^2+1=1+2x\)
\(\Leftrightarrow x^2+y^2-2x=1\)
\(\Leftrightarrow\left(x-1\right)^2+y^2=1\) (C)
Có (C) là đường tròn tâm (1,0) bán kính R=1
Lại có: P=\(\frac{8x+4}{2x-y+1}\)
\(\Leftrightarrow x\left(2P-8\right)-yP+P-4=0\) (Q)
Có (Q) là phương trình đường thẳng.
Để x,y có nghiệm thì đường thẳng và đường tròn giao nhau nghĩa là d(I,(Q))\(\le R\)
\(\Leftrightarrow\frac{\left|x\left(2P-8\right)-yP+P-4\right|}{\sqrt{\left(2P-8\right)^2+P^2}}\le1\)
\(\Leftrightarrow\frac{\left|2P-8+P-4\right|}{\sqrt{\left(2P-8\right)^2+1}}\le1\)
\(\Leftrightarrow\left(3P-12\right)^2\le5P^2-32P+64\)
\(\Leftrightarrow4P^2-40P+80\le0\)
\(\Leftrightarrow5-\sqrt{5}\le P\le5+\sqrt{5}\)
Vậy GTNN của P gần số 3 nhất. Chọn C
VT
14 tháng 9
Bước 1: Phân tích \(2^{2025} + 2\)
Ta có:
\(2^{2025} + 2 = 2 \left(\right. 2^{2024} + 1 \left.\right)\)
Vậy phương trình trở thành:
\(\left(\right. 2 x + y \left.\right) \left(\right. 10 x + 3 y \left.\right) = 2 \left(\right. 2^{2024} + 1 \left.\right)\)
Bước 2: Quan sát tính chẵn/lẻ
- \(2 x + y\) và \(10 x + 3 y\) là các số tự nhiên.
- Hãy xem chúng có thể chia 2 như thế nào.
Gọi \(a = 2 x + y\), \(b = 10 x + 3 y\). Ta có:
\(a \cdot b = 2 \left(\right. 2^{2024} + 1 \left.\right)\)
- Nhận xét: \(2^{2024} + 1\) là số lẻ.
- Vậy \(2 \left(\right. 2^{2024} + 1 \left.\right)\) là số chẵn nhưng không chia hết cho 4.
- Vì \(a \cdot b = 2 \cdot \left(\right. \text{s} \overset{ˊ}{\hat{\text{o}}} \&\text{nbsp};\text{l}ẻ \left.\right)\), nghĩa là một trong hai số \(a\) hoặc \(b\) là chẵn, số còn lại là lẻ.
Bước 3: Thử phân tích
- Nếu \(a = 2\) → \(b = 2^{2024} + 1\)
→ Từ \(a = 2 = 2 x + y\) → \(y = 2 - 2 x\)
→ \(y \geq 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } x = 0 , 1\) - \(x = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } y = 2\)
→ \(b = 10 x + 3 y = 0 + 3 * 2 = 6 \neq 2^{2024} + 1\) → Không được. - \(x = 1 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } y = 0\)
→ \(b = 10 * 1 + 3 * 0 = 10 \neq 2^{2024} + 1\) → Không được.
- \(x = 0 \textrm{ }\textrm{ } \Longrightarrow \textrm{ }\textrm{ } y = 2\)
- Nếu \(b = 2\) → \(a = 2^{2024} + 1\)
→ \(10 x + 3 y = 2\) → Không có nghiệm tự nhiên vì 10x ≥0, 3y ≥0 mà tổng bằng 2.
Bước 4: Kết luận
- Không thể phân tích \(2^{2025} + 2\) thành tích của hai số tự nhiên nhỏ như \(2 x + y\) và \(10 x + 3 y\).
- Vì \(2^{2024} + 1\) là số lẻ rất lớn, không thể biểu diễn dưới dạng \(2 x + y\) với \(x , y \in \mathbb{N}\).
✅ Vậy không tồn tại cặp số tự nhiên \(\left(\right. x , y \left.\right)\) thỏa mãn phương trình.
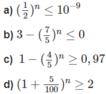
n ≥ log 1 2 10 - 9 ⇔ n ≥ 9 log 2 10 ≈ 29 , 897
Vì n là số tự nhiên bé nhất nên n = 30.