Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) n chia 11 dư 6, chia 17 dư 12, chia 29 dư 24 => n chia 11;17;29 đều thiếu 5
=>n+5 chia hết cho 11;17;29
Vì n nhỏ nhất =>n+5 là BCNN(11;17;29)
Vì 11;17;29 nguyên tố cùng nhau
=>n+5= BCNN(11;17;29)=11x17x29=5423
=>n=5423-5=5418
b) Gọi số tự nhiên cần tìm là x
x chia 13 dư 8, chia 19 dư 14 => x chia 13;19 đều thiếu 5
=> x+5 chia hết cho 13;19 Vì x nhỏ nhất => x+5 là BCNN(13;19)
Vì 13;19 nguyên tố cùng nhau
=> x+5=BCNN(13;19)=13x19=247
=> x+5 thuộc B(247)={0;247;494;741;988;1235;1482;...}
Để có số tận cùng là 7 => x+5 tận cùng là 2 => x+5=1482
x=1482-5
x=1477

chia a cho 17 thì dư 8 =>a+9 chia hết cho 17
chia a cho 25 thì dư 16 =>a+9 chia hết cho 25
=>a+9 chia hết cho 17 và 25
=>a+9 thuộc BC(17;25)
17=17
25=52
=>BCNN(17;25)=17.52=425
=>a+9 thuộc B(425)={0;425;..}
=>a thuộc {-9;416;....}
vì a là số tự nhiên nhỏ nhất có 3 chữ số nên a = 416
chia a cho 17 thì dư 8 thì suy ra a+9 chia hết cho 17
chia a cho 25 thì dư 16 suy ra a+9 chia hết cho 25
suy raa+9 chia hết cho 17 và 25
suy raa+9 thuộc BC(17;25)
17 = 17 vì 17 là số nguyên tố
25 = 52
suy ra BCNN(17;25)=17.52=425
suy ra a+9 thuộc B(425)={0;425;..}
suy ra a thuộc {-9;416;....}
vì a là số tự nhiên nhỏ nhất có 3 chữ số nên a = 416
vậy a = 416
**** cho mình nhé

a +8 chia hết cho 24 và 27
a nhỏ nhất
=> a+8 =BCNN(24;27) =216
=> a =216 -8
a =208
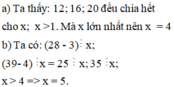


Theo đề ra, ta có:
\(\hept{\begin{cases}\left(a+7\right)⋮28\\\left(a+7\right)⋮24\\\left(a+7\right)⋮16\end{cases}}\Rightarrow\left(a+7\right)\in BC\left(28;24;16\right)\)
Ta có:
\(28=2^2.7\)
\(24=2^3.3\)
\(16=2^4\)
\(\Rightarrow BCNN\left(16;18;24\right)=2^4.3.7=336\)
\(\Rightarrow\left(a+7\right)=BC\left(16;18;24\right)=\left\{0;336;672;1008;...\right\}\)
Mà đề ra a là số nhỏ nhất có bốn chữ số
\(a+7=1008\Rightarrow a=1008-7\Rightarrow a=1001\)