K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
BA
19 tháng 6 2019
1.Tìm x , biết
.2x -1/2-1/6-1/12-...- 1/49*50=7-1/50+x
=> 2x- ( 1/2+1/6+1/12+...1/ 49.50 )= 7-1/50+x
=> 2x -( 1/1.2 + 1/2.3+1/3.4+...+1/49.50)= 7-1/50+x
=> 2x - ( 1- 1/2+ 1/2-1/3+1/3-1/4+...+1/49-1/50) = 7-1/50 + x
=> 2x - ( 1-1/50) =7-1/50 + x
=> 2x- 1+ 1/50=7-1/50+ x
=> 1+1/50= 2x- (7 - 1/50+ x)
=> 1+1/50 = 2x- 7 + 1/50- x
=> 1+1/50 = x + 1/50 - 7
=> 1 = x + 1/50 - 7 - 1/50
=> 1 = x - 7
=> x = 8
Vậy...
Tham khảo thêm:Câu hỏi của Cừu beta - Toán lớp 7 - Học toán với OnlineMath
BA
19 tháng 6 2019
LinkCâu hỏi của Cừu beta - Toán lớp 7 - Học toán với OnlineMath
HV
0
T
28 tháng 11 2023
Giup mình với ah.
1- Tính :
A= 5. | x- 5 | - 3x + 1
2 - Tìm các số nguyên x,y ; sao cho :
a) 5/x - y/3 = 1/6 b) 5/x + y/4 = 1/8
3- Tìm giá trị lớn nhất của Q = 27-2x/12-x ( x là số nguyên)
---------------------------------------------------------------------------------------------
NT
0
28 tháng 11 2023
1) \(A=5.\left|x-5\right|-3x+1\)
\(A=\left[{}\begin{matrix}5.\left(x-5\right)-3x+1\left(x-5\ge0\right)\\5.\left(5-x\right)-3x+1\left(x-5< 0\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}5x-25-3x+1\left(x\ge5\right)\\25-5x-3x+1\left(x< 5\right)\end{matrix}\right.\)
\(A=\left[{}\begin{matrix}2x-24\left(x\ge5\right)\\26-8x\left(x< 5\right)\end{matrix}\right.\)
29 tháng 11 2023
3:
\(Q=\dfrac{27-2x}{12-x}=\dfrac{2x-27}{x-12}\)
\(\Leftrightarrow Q=\dfrac{2x-24-3}{x-12}=2-\dfrac{3}{x-12}\)
Để Q lớn nhất thì \(2-\dfrac{3}{x-12}\) lớn nhất
=>\(\dfrac{3}{x-12}\) nhỏ nhất
=>x-12 là số nguyên âm lớn nhất
=>x-12=-1
=>x=11
Vậy: \(Q_{min}=2-\dfrac{3}{11-12}=2+3=5\) khi x=11
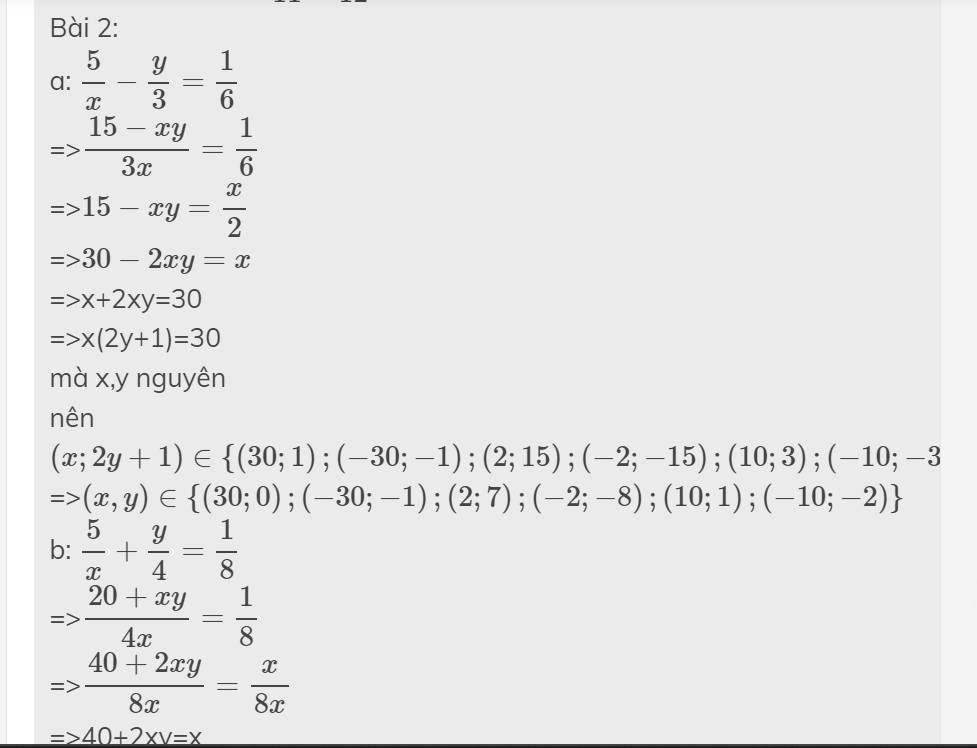
Bài 2:
a: \(\dfrac{5}{x}-\dfrac{y}{3}=\dfrac{1}{6}\)
=>\(\dfrac{15-xy}{3x}=\dfrac{1}{6}\)
=>\(15-xy=\dfrac{x}{2}\)
=>\(30-2xy=x\)
=>x+2xy=30
=>x(2y+1)=30
mà x,y nguyên
nên \(\left(x;2y+1\right)\in\left\{\left(30;1\right);\left(-30;-1\right);\left(2;15\right);\left(-2;-15\right);\left(10;3\right);\left(-10;-3\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(30;0\right);\left(-30;-1\right);\left(2;7\right);\left(-2;-8\right);\left(10;1\right);\left(-10;-2\right)\right\}\)
b: \(\dfrac{5}{x}+\dfrac{y}{4}=\dfrac{1}{8}\)
=>\(\dfrac{20+xy}{4x}=\dfrac{1}{8}\)
=>\(\dfrac{40+2xy}{8x}=\dfrac{x}{8x}\)
=>40+2xy=x
=>x-2xy=40
=>x(1-2y)=40
mà x,y nguyên
nên \(\left(x;1-2y\right)\in\left\{\left(40;1\right);\left(-40;-1\right);\left(8;5\right);\left(-8;-5\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(40;0\right);\left(-40;1\right);\left(8;-2\right);\left(-8;3\right)\right\}\)
21 tháng 1 2019
\(1)\)
\(VT=\left(\left|x-6\right|+\left|2022-x\right|\right)+\left|x-10\right|+\left|y-2014\right|+\left|z-2015\right|\)
\(\ge\left|x-6+2022-x\right|+\left|0\right|+\left|0\right|+\left|0\right|=2016\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(\hept{\begin{cases}\left(x-6\right)\left(2022-x\right)\ge0\left(1\right)\\x-10=y-2014=z-2015=0\left(2\right)\end{cases}}\)
\(\left(2\right)\)\(\Leftrightarrow\)\(\hept{\begin{cases}x=10\\y=2014\\z=2015\end{cases}}\)
\(\left(1\right)\)
TH1 : \(\hept{\begin{cases}x-6\ge0\\2022-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge6\\x\le2022\end{cases}\Leftrightarrow}6\le x\le2022}\) ( nhận )
TH2 : \(\hept{\begin{cases}x-6\le0\\2022-x\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le6\\x\ge2022\end{cases}}}\) ( loại )
Vậy \(x=10\)\(;\)\(y=2014\) và \(z=2015\)
21 tháng 1 2019
\(2)\)
\(VT=\left|x-5\right|+\left|1-x\right|\ge\left|x-5+1-x\right|=\left|-4\right|=4\)
\(VP=\frac{12}{\left|y+1\right|+3}\le\frac{12}{3}=4\)
\(\Rightarrow\)\(VT\ge VP\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(\hept{\begin{cases}\left(x-5\right)\left(1-x\right)\ge0\left(1\right)\\\left|y+1\right|=0\left(2\right)\end{cases}}\)
\(\left(1\right)\)
TH1 : \(\hept{\begin{cases}x-5\ge0\\1-x\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ge5\\x\le1\end{cases}}}\) ( loại )
TH2 : \(\hept{\begin{cases}x-5\le0\\1-x\le0\end{cases}\Leftrightarrow\hept{\begin{cases}x\le5\\x\ge1\end{cases}\Leftrightarrow}1\le x\le5}\) ( nhận )
\(\left(2\right)\)\(\Leftrightarrow\)\(y=-1\)
Vậy \(1\le x\le5\) và \(y=-1\)
TT
3
A
19 tháng 8 2020
Ta có : \(\frac{1}{x}-\frac{y}{6}=\frac{1}{3}\Leftrightarrow\frac{1}{x}=\frac{1}{3}+\frac{y}{6}\Leftrightarrow\frac{1}{x}=\frac{2+y}{6}\)
\(\Leftrightarrow\left(2+y\right)x=6\Leftrightarrow2+y;x\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| x | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| 2 + y | 6 | -6 | 3 | -3 | 2 | -2 | 1 | -1 |
| y | 4 | -8 | 1 | -5 | 0 | -4 | -1 | -3 |
19 tháng 8 2020
\(\frac{1}{x}-\frac{y}{6}=\frac{1}{3}\)
\(\Rightarrow\frac{1}{x}=\frac{1}{3}+\frac{y}{6}\)
\(\Rightarrow\frac{1}{x}=\frac{2}{6}+\frac{y}{6}\)
\(\Rightarrow\frac{1}{x}=\frac{2+y}{6}\)
\(\Rightarrow x\left(2+y\right)=6\)
Ta có bảng sau :
| x | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| 2+y | 6 | -6 | 3 | -3 | 2 | -2 | 1 | -1 |
| y | 4 | -8 | 1 | -5 | 0 | -4 | -1 | -3 |
Vậy ( x ; y ) = { ( 1 ; 4 ) , ( -1 ; -8 ) , ( 2 ; 1 ) , ( -2 ; -5 ) , ( 3 ; 0 ) , ( -3 ; -4 ) , ( 6 ; -1 ) , ( -6 ; -3 ) }