Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho tam giác abc và 2 điểm M,N thỏa mãn điều kiện MA+3MC=0,NA+2NB+3NC=0,chưmgs minh b,m,n thẳng hàng

vecto NA+2*vecto NB+3*vecto NC=vecto 0
=>2*vecto NB=-vecto NA-3 vecto NC
=>vecto NB=-1/2*vecto NA-3/2*vecto NC
=-1/2(vecto NM+vecto MA)-3/2(vecto NM+vecto MC)
=-2vecto NM-1/2vecto MA-3/2vecto MC
=-2 vecto NM-1/2(vecto MA+3 vecto MC)
=-2 vecto NM
=>vecto BN=2*vecto MN
=>B,M,N thẳng hàng

1: TH1: m=0
=>-x-2=0
=>x=-2(loại)
TH2: m<>0
\(\text{Δ}=\left(2m-1\right)^2-4m\left(m-2\right)\)
=4m^2-4m+1-4m^2+8m
=4m+1
Đểphương trình có 2 nghiệm pb thì 4m+1>0
=>m>-1/4
2: TH1: m=1
Pt sẽ là -2x-1=0
=>x=-1/2(nhận)
TH2: m<>1
\(\text{Δ}=\left(-2m\right)^2-4\left(m-1\right)\left(m-2\right)\)
=4m^2-4(m^2-3m+2)
=-4(-3m+2)
=12m-8
Để phương trình có 1 nghiệm thì 12m-8=0
=>m=2/3

câu 2:
a) Trước tiên ta chứng minh f đơn ánh. Thật vậy nếu f (n1) = f (n2) thì
f (f(n1) + m) = f (f(n2) + m)
→n1 + f(m + 2003) = n2 + f(m + 2003) → n1 = n2
b) Thay m = f(1) ta có
f (f(n) + f(1)) = n + f (f(1) + 2003)
= n + 1 + f(2003 + 2003)
= f (f(n + 1) + 2003)
Vì f đơn ánh nên f(n)+f(1) = f(n+1)+2003 hay f(n+1) = f(n)+f(1)−2003. Điều này dẫn đến
f(n + 1) − f(n) = f(1) − 2003, tức f(n) có dạng như một cấp số cộng, với công sai là f(1) − 2003,
số hạng đầu tiên là f(1). Vậy f(n) có dạng f(n) = f(1) + (n − 1) (f(1) − 2003), tức f(n) = an + b.
Thay vào quan hệ hàm ta được f(n) = n + 2003, ∀n ∈ Z
+.
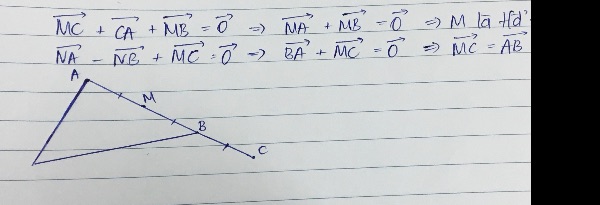


a) \(\left(n+1\right)\left(n+3\right)=0\)
\(\Rightarrow n+1=0\) hoặc \(n+3=0\)
+) \(n+1=0\Rightarrow n=-1\)
+) \(n+3=0\Rightarrow n=-3\)
Vậy \(n\in\left\{-1;-3\right\}\)
b) \(\left(\left|n\right|+2\right)\left(n^2-1\right)=0\)
\(\Rightarrow\left|n\right|+2=0\) hoặc \(n^2-1=0\)
+) \(\left|n\right|+2=0\Rightarrow\left|n\right|=-2\) ( loại )
+) \(n^2-1=0\Rightarrow n^2=1\Rightarrow n=1\) hoặc \(n=-1\)
Vậy \(n\in\left\{1;-1\right\}\)