Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.

Đáp án A
Mệnh đề 1) sai vì f ' x 0 = 0 chỉ là điều kiện cần chưa là điều kiện đủ để hàm số đạt cực trị tại x 0
Mệnh đề 2) Sai vì khi f ' x 0 = f ' ' x 0 = 0 có thể hàm số có thể đạt cực trị hoặc không đạt cực trị tại x 0 .
Mệnh đề 3) sai vì f ' x đổi dấu qua điểm x 0 thì điểm x 0 có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.
Mệnh đề 4) Sai vì trong trường hợp này x 0 là điểm cực tiểu của đồ thị hàm số.

Đáp án A
A sai vì hàm số y = x 3 có y ' 0 = 0 nhưng không đạt cực trị tại x = 0
B sai vì hàm số y = x 4 có y ' 0 = 0 , y ' ' 0 = 0 đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = f ' ' x 0 = 0 thì điểm x 0 nhưng không đạt cực trị tại x = 0
C sai vì “Nếu f ' x đổi dấu khi x qua x 0 thì điểm x 0 là điểm trị (cực đại và cực tiểu) của hàm số y = f ' ' x
D sai vì “Nếu hàm số y = f x có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = 0 ; f ' ' x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f ' ' x

ta tính \(y'=6x^2+a-12\)
để hàm số vừa có cực đại và cực tiểu thì \(y'=0\) hai nghiệm phân biệt suy ra \(6x^2+a-12=0\Leftrightarrow6x^2=12-a\) (*)
để (*) có 2 nghiệm phân biệt thì \(12-a>0\Leftrightarrow a<12\)
vậy với a<12 thì hàm số có cực đại và cực tiểu
gọi \(x_1;x_2\) là cực đại và cực tiểu của hàm số
suy ra \(x_{1,2}=\pm\sqrt{\frac{12-a}{6}}\) ta thay vào hàm số suy ra đc \(y_{1,2}\) suy ra \(I\left(x_1;y_1\right);A\left(x_2;y_2\right)\)
sử dụng công thức tính khoảng cách
pt đường thẳng y có dạng x=0
ta có \(d\left(I;y\right)=\frac{\left|x_1\right|}{\sqrt{1}}\); \(d\left(A;y\right)=\frac{\left|x_2\right|}{\sqrt{1}}\)
\(d\left(I,y\right)=d\left(A,y\right)\) giải pt ta tìm ra đc a

Đáp án D
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]

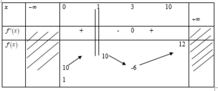

Đáp án A
Có 2 mệnh đề sai là mệnh đề (3) và mệnh đề (4).
Mệnh đề (3) sai vì nếu hai cực trị của hàm số cùng dấu thì đồ thị hàm số chỉ cắt trục Ox tại một điểm.
Mệnh đề (4) sai lý do tương tự mệnh đề (3).