Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số đầu là x.
Cấp số cộng là q.
=> Số đầu, thứ 2. 3,4,5 là x,x+q,x+2q,x+3q,x+4q.
Tổng số 1 và 3 là x + (x+2q) = 28
Tổng số 3 và cuối là (x+2q)+(x+4q)=40.
Ta đã có 2 phương trình tạo thành 1 hệ phương trình.
Giải hệ tìm x và q.
Chúc em học tốt!

Gọi cấp số nhân tăng nghiêm ngặt là \(a_n\). Theo đầu bài ta có \(a_2,a_4\) là 2 nghiệm của phương trình
\(t^2-30t+144=0\Leftrightarrow\begin{cases}t=6\\t=24\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2=6\\a_4=24\end{cases}\) hoặc \(\begin{cases}a_2=24\\a_4=6\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1q=6\\a_1q^3=24\end{cases}\) hoặc \(\begin{cases}a_1q=24\\a_1q^3=6\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1q=6\\q^2=4\end{cases}\) hoặc \(\begin{cases}a_1q=24\\q^2=\frac{6}{24}=\frac{1}{4}\end{cases}\)
\(\Leftrightarrow\begin{cases}a_1=\frac{6}{\pm2}\\q=\pm2\end{cases}\) hoặc \(\begin{cases}a_1=24\left(\pm2\right)\\q=\pm\frac{1}{2}\end{cases}\)
Do cấp số nhân tăng nghiêm ngặt, nên q>1, do vậy ta chọn \(a_1=3;q=2\)
Cho nên \(S_{10}=u_1\frac{2^{10}-1}{2-1}=3.\left(1024-1\right)=3069\)
Giao lưu:
Gọi dãy số đã co có dạng: \(U_1;U_2;U_3;U_4;U_5...U_{10}...U_n\)
đầu bài ta có hệ phương trình.
\(\left\{\begin{matrix}U_n.q=U_{\left(n+1\right)}\left(1\right)\\q>1\left(2\right)\\U_2+U_4=144\left(3\right)\\U_2.U_4=30\left(4\right)\end{matrix}\right.\)
Thế (3) vào (4) \(\Leftrightarrow U_2\left(144-U_2\right)=30\Leftrightarrow U_2^2-144U_4+30=0\Rightarrow\left[\begin{matrix}U_2=24\\U_2=6\end{matrix}\right.\)
Vì U2 và U4 có vai trò như nhau
do vậy có cắp nghiệm là hoán đổi (U2,U4)=(6,24)(*)
Từ (1) và (2) ta có(*)=> \(\left\{\begin{matrix}U_2=6\\U_4=24\end{matrix}\right.\)(**)
Từ (1) ta có: \(U_4=q.U_3=q.\left(q.U_2\right)=q^2.U_2\)(4)
Từ (**) và (4) ta có \(\frac{U_4}{U_2}=q^2=\frac{24}{6}=4\Rightarrow!q!=2\) (5)
Từ (3) và (5) => q=2
Vậy tổng 10 số hạng đầu tiên của dẫy là :\(S_{10}=2^0.3+2^1.3+3.2^2+...+3.2^8+3.2^9=3.\left(1+2+2^2+..+2^9\right)\)
\(S_{10}=3.\left(2^{10}-1\right)\)

Đáp án là C. Vì:
Gọi d là công bội của dãy cấp số nhân \((u_n) \)
⇒ \(u_n=d.u_{n-1}=d^2.u_{n-2}=...=d^{n-2}.u_2=d^{n-1}.u_1\)
Suy ra: \(u_5=d^3.u_2 \Rightarrow d^3=\dfrac{u_5}{u_2}=\dfrac{48}{6}=8 \Rightarrow d=2\)
Có: \(u_2=d.u_1 \Leftrightarrow u_1=\dfrac{u_2}{d}=\dfrac{6}{2}=3\)
Theo đề: \(u_1+u_2+...+u_n=381 \)
\(\Leftrightarrow u_1+d.u_1+d^2.u_1+...+d^{n-1}u_1=381\)
\(\Leftrightarrow u_1(1+d+d^2+...+d^{n-1})=381\)
Mặt khác: \(u_1(1+d+d^2+...+d^{n-1})=3.\dfrac{d^n-1}{d-1} =3.\dfrac{2^n-1}{2-1}=3.(2^n-1)\)
\(\Rightarrow 3.(2^n-1)=381 \Leftrightarrow 2^n-1=127 \Leftrightarrow 2^n=128=2^7 \Rightarrow n=7\).
Vậy n = 7 thuộc (6;11)

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
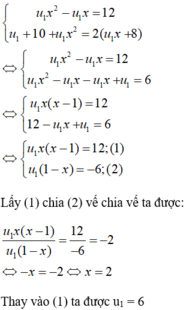
+ Tổng của năm số hạng đầu của CSN là:


Chọn A
Gọi u1,u2,u3,u4 là 4 số hạng đầu tiên của cấp số nhân, với công bội q. gọi (vn) là cấp số cộng tương ứng với công sai là d. Theo giả thuyết Ta có:
u 1 + u 2 + u 3 = 16 4 9 u 1 = v 1 u 2 = v 4 = v 1 + 3 d u 3 = v 8 = v 1 + 7 d ⇔ u 1 + u 1 q + u 2 q 2 = 16 4 9 1 u 1 q = u 1 + 3 d 2 u 1 q 2 = u 1 + 7 d 3
Khử d từ (2) và (3) ta thu được:
7 u 1 q = 7 u 1 + 21 d 3 u 1 q 2 = 3 u 1 + 21 d
Lấy vế trừ vế ta thu được
7 u 1 q − 3 u 1 q 2 = 4 u 1 ⇔ u 1 . 3 q 2 − 7 q + 4 = 0 ⇔ u 1 = 0 3 q 2 − 7 q + 4 = 0
Do u 1 ≠ 0 ⇒ q = 1 q = 4 3
Theo định nghĩa cấp số nhận thì q ≠ 1 . Do đó q = 4 3
Thay q = 4 3 vào (1) ta được u 1 = 4
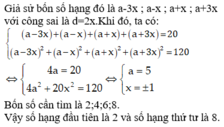
Bạn kiểm tra lại đề bài, phải là csn lùi vô hạn thì mới tính được
a/ \(S=\dfrac{u_1}{1-q}=32;u_2=u_1.q=8\)
\(\Rightarrow\dfrac{\dfrac{8}{q}}{1-q}=32\Leftrightarrow q=\dfrac{1}{2}\Rightarrow u_1=\dfrac{8}{\dfrac{1}{2}}=16\)
\(\Rightarrow u_n=16.\left(\dfrac{1}{2}\right)^{n-1}=32.\left(\dfrac{1}{2}\right)^n\)
b/ \(S_3=u_1+u_2+u_3=\dfrac{39}{25};S=\dfrac{u_1}{1-q}=\dfrac{5}{3}\)
\(S_3=u_1+u_1.q+u_1q^2=\dfrac{39}{25}\Leftrightarrow u_1\left(1+q+q^2\right)=\dfrac{39}{25}\)
\(\Rightarrow u_1=\dfrac{39}{25\left(1+q+q^2\right)}\Rightarrow\dfrac{\dfrac{39}{25\left(1+q+q^2\right)}}{1-q}=\dfrac{5}{3}\)
\(\Leftrightarrow q=...\Rightarrow u_1=...\Rightarrow u_n=u_1.q^{n-1}\)
P/s: Bạn tự làm nốt ạ