FH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TK
14 tháng 8
Bài giải
Gọi hệ trục Oxyz với A(0;0;0), B(a;0;0), C(a;a;0), D(0;a;0). Gọi S(p;q;h).
SA = SB = a:
p² + q² + h² = a²
(p - a)² + q² + h² = a² ⇒ p = a/2
SC = a√3:
a²/4 + (q - a)² + h² = 3a²
Từ SA: q² + h² = 3a²/4 ⇒ a²/4 + q² - 2aq + a² + h² = 3a²
2a² - 2aq = 3a² ⇒ q = -a/2 ⇒ h² = a²/2 ⇒ h = a√2/2
S(a/2; -a/2; a√2/2)
H(a/4; -a/4; a√2/4), K(3a/4; -a/4; a√2/4)
M(x; x; 0), 0 ≤ x ≤ a
N(a; t; 0) ∈ BC
HK = (a/2; 0; 0)
HM = (x - a/4; x + a/4; -a√2/4)
n = HK × HM = (0; a²√2/8; a/2(x + a/4))
Mặt phẳng (HKM): (a²√2/8)(y + a/4) + (a/2)(x + a/4)(z - a√2/4) = 0
Với N(a; t; 0): t = x ⇒ N(a; x; 0)
HK = a/2, MN = a - x
d = √[(x + a/4)² + a²/8]
S = (a/2 + a - x)/2 × d = (3a/2 - x)/2 × √[(x + a/4)² + a²/8]
Giải S'(x) = 0 ⇒ x = 5a/8
Kết luận: x = 5a/8 thì diện tích HKMN nhỏ nhất
Cho mình xin 1 tick với ạ
14 tháng 12 2021
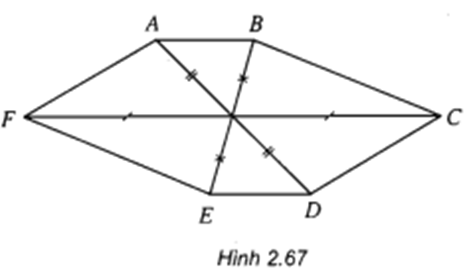
Hai tam giác CBA và DBA là hai tam giác đều cạnh a
=> ∆ CBA = ∆ DBA ( c.c.c)
=> CM = DM ( 2 đường trung tuyến tương ứng)
=> Tam giác CMD cân tại M.
Lại có: MN là đường trung tuyến nên đồng thời là đường cao: MN ⊥ CD
* Chứng minh tương tự, ta có: MN ⊥ AB
Do đó, MN là đoạn vuông góc chung của AB và CD.
* Tam giác BCD là tam giác đều cạnh a nên
\(BN=\sqrt{BC^2-CN^2}=\frac{a\sqrt{3}}{2}\)
Bài này học rồi mà bà
HA
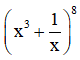
(x4 – x2 + x - 1) =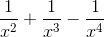 
) = +∞.
(-2x3 + 3x2 -5 ) =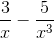 
) = +∞.
= 
= +∞.
= 
= 
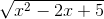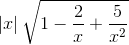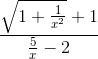= -1.
16 tháng 11 2021
Gọi mỗi số là abcd
d có 2 cách
a có 5 cách a#0
b có 5 cách b#a
c có 4 cách c#b,a
Nếu sai sót dì thông càm
Ta có: (x3 +
)8=Ck8 x3(8 – k) ()k =Ck8 x24 – 4k
Trong tổng này, số hạng Ck8 x24 – 4k không chứa x khi và chỉ khi