Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2, sin4x+cos5=0 <=> cos5x=cos\(\left(\frac{\pi}{2}+4x\right)\Leftrightarrow\orbr{\begin{cases}x=\frac{\pi}{2}+k2\pi\\x=-\frac{\pi}{18}+\frac{k2\pi}{9}\end{cases}\left(k\inℤ\right)}\)
ta có \(2\pi>0\Leftrightarrow k< >\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(\frac{\pi}{2}\)khi k=0
\(-\frac{\pi}{18}+\frac{k2\pi}{9}>0\Leftrightarrow k>\frac{1}{4}\)do k nguyên nên nghiệm dương nhỏ nhất trong họ nghiệm \(-\frac{\pi}{18}-\frac{k2\pi}{9}\)là \(\frac{\pi}{6}\)khi k=1
vậy nghiệm dương nhỏ nhất của phương trình là \(\frac{\pi}{6}\)
\(\frac{\pi}{2}+k2\pi< 0\Leftrightarrow k< -\frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(\frac{\pi}{2}+k2\pi\)là \(-\frac{3\pi}{2}\)khi k=-1
\(-\frac{\pi}{18}+\frac{k2\pi}{9}< 0\Leftrightarrow k< \frac{1}{4}\)do k nguyên nên nghiệm âm lớn nhất trong họ nghiệm \(-\frac{\pi}{18}+\frac{k2\pi}{9}\)là \(-\frac{\pi}{18}\)khi k=0
vậy nghiệm âm lớn nhất của phương trình là \(-\frac{\pi}{18}\)

Lời giải:
Ta có:
\(f'(x)=3x^2+2(a-1)x+2\)
Theo định lý về dấu của tam thức bậc 2, để \(f'(x)>0\) với mọi \(x\in\mathbb{R}\) thì \(\Delta'=(a-1)^2-6<0\)
\(\Leftrightarrow -\sqrt{6}< a-1< \sqrt{6}\)
\(\Leftrightarrow 1-\sqrt{6}< a< 1+\sqrt{6}\)
Đáp án B

lim (x-->0) \(\frac{\sqrt[3]{ax+1}-\sqrt{1-bx}}{x}=2\)
<=> lim ( x-->0) \(\left(\frac{\sqrt[3]{ax+1}-1}{x}+\frac{1-\sqrt{1-bx}}{x}\right)=2\)
<=> lim (x-->0)\(\left(\frac{a}{\sqrt[3]{\left(ax+1\right)^2}+\sqrt[3]{ax+1}+1}+\frac{b}{\sqrt{1-bx}+1}\right)=2\)
<=> \(\frac{a}{3}+\frac{b}{2}=2\)
mà a + 3b = 3
=> a= 3; b = 2
=> A là đáp án sai.

\(\lim\limits_{x\rightarrow-\infty}\left(4x^5-3x^2+1\right)=\lim\limits_{x\rightarrow-\infty}x^5\left(4-\frac{3}{x^3}+\frac{1}{x^5}\right)=-\infty.4=-\infty\)
\(\lim\limits_{x\rightarrow4}\frac{1-x}{\left(x-4\right)^2}=\frac{-3}{0}=-\infty\)
Câu tiếp theo đề thiếu, ko thấy yêu cầu gì hết
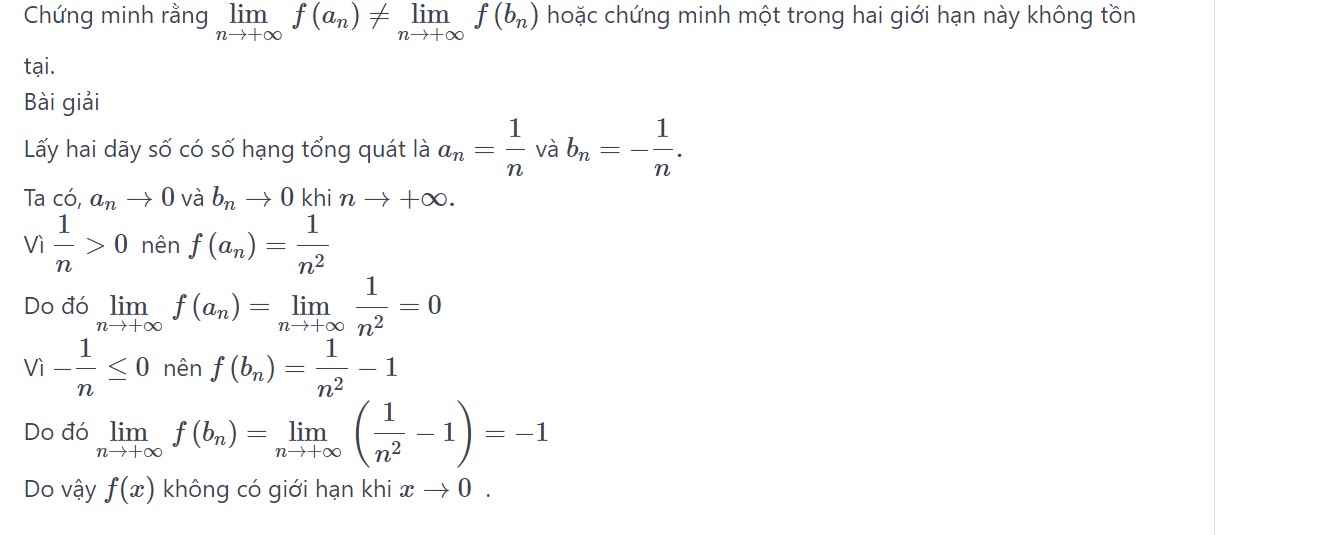
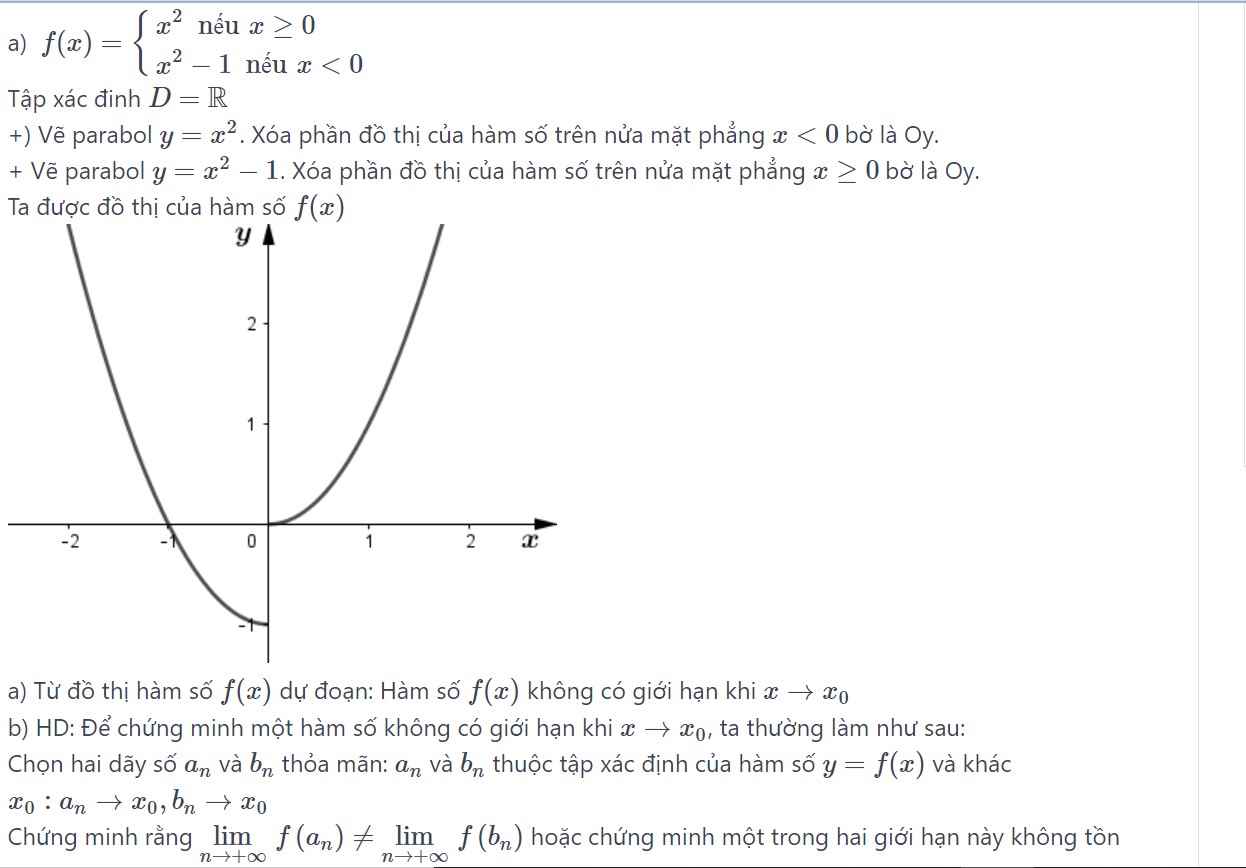
Chọn A.
Ta có: f’(x) = 3x2 – 6x.
f’(x) < 0 ⇔ 3x2 – 6x < 0 ⇔ 0 < x < 2.