
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài 2
22...2^33...3 + 33...3^22...2
= 22...2^33..32 . 22...2 + 33...3^22..20 . 33...3^3
= (...6) . (...2) + (...1) . (...7)
= (...2) + (...7)
= (...9)
=> chia 5 dư 4

1/
a chia 4 dư 3 => a - 1 chia hết cho 4
a chia 5 dư 4 => a - 1 chia hết cho 5
a chia 6 dư 5 => a - 1 chia hết cho 6
=> a - 1 \(\in\)BC (4, 5, 6)
4 = 22
5 = 5
6 = 2 . 3
BCNN (4, 5, 6) = 22 . 5 . 3 = 60
BC (4, 5, 6) = B (60) = {0 ; 60 ; 120 ; 180 ; ...}
Vậy a \(\in\){59 ; 119 ; 179 ; ...}
mà a chia hết cho 13 nên chọn a = 299.
Vậy a = 299.
2/ Vì a là số có ba chữ số nên dạng tổng quát của a là abc.

20174n có tận cùng là 1 ; 2015n có tận cùng là 5.
Ta có: A = 20172016-20152014 = 20174.504-20152014 = (...1)-(...5) = (...6)
A có chữ số tận cùng là 6 nên khi chia A cho 5 sẽ dư 1
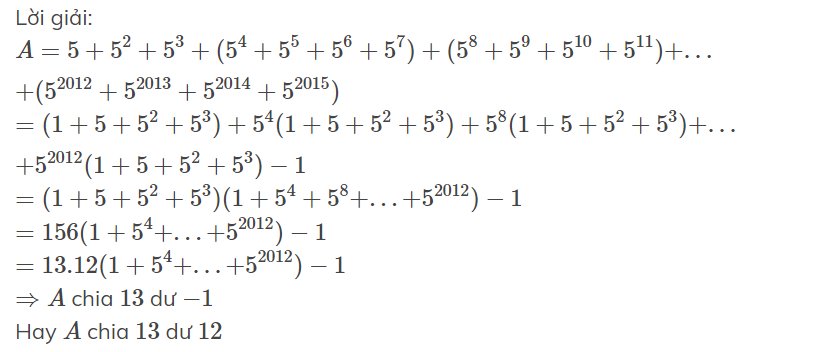
Lời giải:
$A=5+5^2+5^3+(5^4+5^5+5^6+5^7)+(5^8+5^9+5^{10}+5^{11})+...+(5^{2012}+5^{2013}+5^{2014}+5^{2015})$
$=(1+5+5^2+5^3)+5^4(1+5+5^2+5^3)+5^8(1+5+5^2+5^3)+...+5^{2012}(1+5+5^2+5^3)-1$
$=(1+5+5^2+5^3)(1+5^4+5^8+...+5^{2012})-1$
$=156(1+5^4+...+5^{2012})-1$
$=13.12(1+5^4+...+5^{2012})-1$
$\Rightarrow A$ chia $13$ dư $-1$
Hay $A$ chia $13$ dư $12$